Ричард Фейнман - Том 2. Электромагнетизм и материя

Задача 1. Если мы приложим к концам бруска давление р , то деформация сжатия будет отрицательна и равна p / Y :

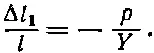
Задача 2. Если мы надавим на горизонтальные грани бруска, то деформация по высоте будет равна - p / Y , а соответствующая деформация в боковом направлении будет +σ p / Y . Мы получаем

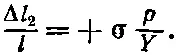
Задача 3. Если мы приложим к сторонам бруска давление р , то деформация давления снова будет равна p / Y , но теперь нам нужно определить деформацию длины. Для этого боковую деформацию нужно умножить на -σ. Боковая деформация равна

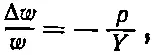
так что

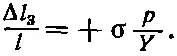
Комбинируя результаты этих трех задач, т. е. записывая Δl как Δl 1+Δl 2+Δl 3, получаем

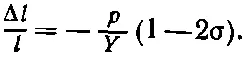(38.6)

Задача, разумеется, симметрична во всех трех направлениях, поэтому

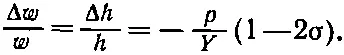(38.7)

Интересно также найти изменение объема при гидростатическом давлении. Поскольку V = lwh , то для малых перемещений можно записать

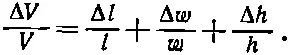
Воспользовавшись (38.6) и (38.7), мы имеем

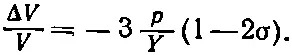(38.8)

Имеются любители называть ΔV/V объемной деформацией и писать

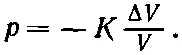
Объемное напряжение р (гидростатическое давление) пропорционально вызванной им объемной деформации — снова закон Гука. Коэффициент К называется объемным модулем и связан с другими постоянными выражением

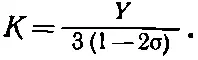(38.9)

Поскольку коэффициент К представляет некоторый практический интерес, то во многих справочниках вместо Y и σ приводятся Y и К . Но если вам нужно знать σ, то вы всегда можете получить это значение из формулы (38.9). Из этой формулы видно также, что коэффициент Пуассона σ должен быть меньше 1/ 2. Если бы это было не так, то объемный модуль К был бы отрицательным и материал при увеличении давления расширялся бы. Это позволило бы добывать механическую энергию из любого кубика, т. е. это означало бы, что кубик находится в неустойчивом равновесии. Если бы он начал расширяться, то расширение продолжалось бы само по себе с высвобождением энергии.

Посмотрим, что получится, если мы приложим к чему-то «косое» напряжение. Под косым, или скалывающим, напряжением мы подразумеваем такое воздействие, как показано на фиг. 38.4.

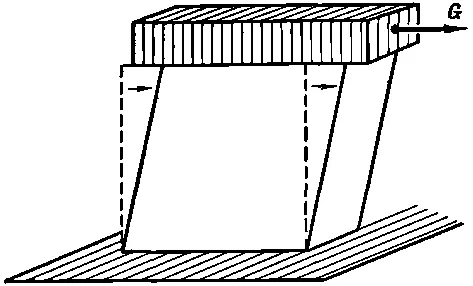
Фиг. 38.4. Однородный сдвиг.

В качестве предварительной задачи посмотрим, какова будет деформация кубика под действием сил, показанных на фиг. 38.5.

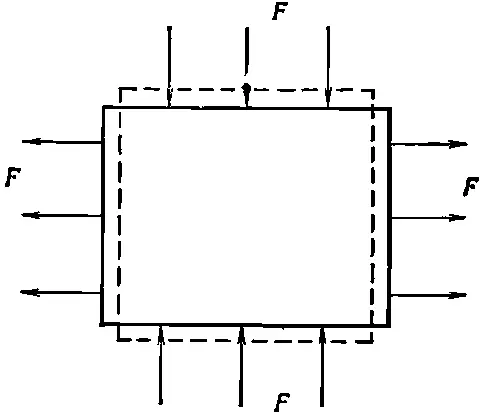
Фиг. 38.5. Действие сжимающих сил, давящих на вершину и основание, и равных им растягивающих сил с двух сторон.

Снова можно разделить эту задачу на две: вертикальное давление и горизонтальное растяжение. Обозначая через А площадь грани кубика, мы получаем для изменения горизонтальной длины

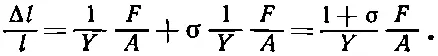(38.10)

Изменение же высоты по вертикали равно просто тому же выражению с обратным знаком.

Предположим теперь, что мы имеем тот же самый кубик, и подвергнем его действию сдвиговых сил, показанных на фиг. 38.6, а .

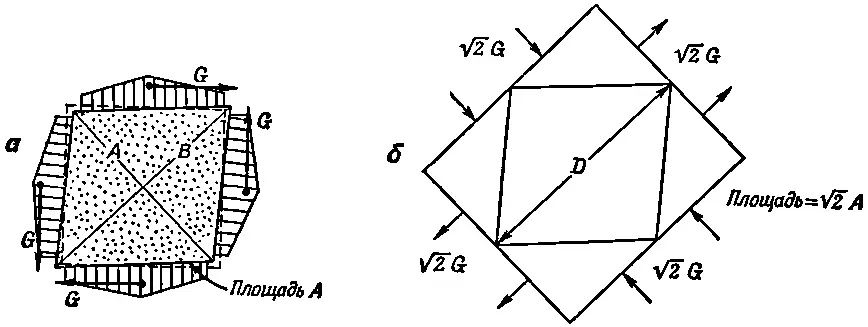
Фиг. 38.6. Две пары сил сдвига (а) создают то же самое напряжение, что и сжимающие=растягивающие силы (б).

Заметим теперь, что все силы должны быть равными, ибо на тело не должен действовать никакой момент сил и оно должно находиться в равновесии. (Подобные силы должны действовать также и в случае, изображенном на фиг. 38.4, поскольку кубик находится в равновесии. Они обеспечиваются тем, что кубик «приклеен» к столу.) При таких условиях говорят, что кубик находится в состоянии чистого сдвига. Но обратите внимание, что если мы разрежем кубик плоскостями под углом 45°, скажем, вдоль диагонали А на фиг. 38.6, а, то полная сила, действующая в этой плоскости, нормальна к ней и равна √2G. Площадь, на которой действует эта сила, равна √2A; следовательно, напряжение, нормальное к этой плоскости, будет просто G / A . Точно так же если взять плоскость, наклоненную под углом 45° в другую сторону, т. е. по диагонали В , то мы увидим, что на ней действует нормальное сдавливающее напряжение, равное - G / A . Из этого ясно, что напряжение при «чистом сжатии» эквивалентно комбинации растягивающего и сжимающего напряжений, направленных под прямым углом друг к другу и под углом 45° к первоначальным граням кубика. Внутренние напряжения и деформации будут такими же, как и в большом кубике материала под действием сил, показанных на фиг. 38.6, б . Но эту задачу мы уже решили. Изменение длины диагонали задается уравнением (38.10):

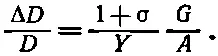(38.11)

(Одна диагональ сокращается, а другая удлиняется.)

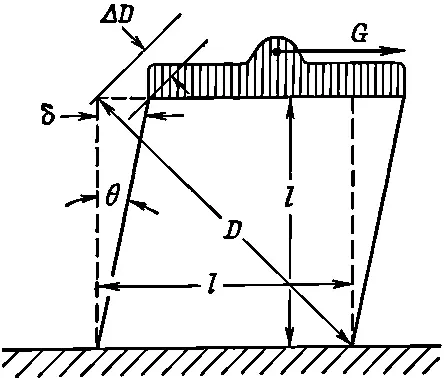
Часто деформацию сдвига удобно описывать с помощью угла «искажения» кубика θ, показанного на фиг. 38.7.