Ричард Фейнман - Том 2. Электромагнетизм и материя

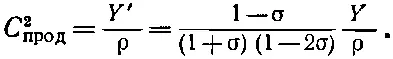(38.33)

Поскольку значение σ заключено между 0 и 1/ 2, то модуль сдвига μ меньше модуля Юнга Y , а Y ', кроме того, больше Y, так что

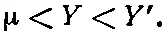
Это означает, что продольные волны распространяются быстрее, чем волны сдвига. Один из наиболее точных способов определения упругих постоянных вещества дает измерение плотности материала и скоростей двух сортов волн. Из этой информации можно получить как Y, так и σ. Кстати, именно измеряя разность во времени прихода двух сортов волн от землетрясения, сейсмологи только по сигналам, принятым одной станцией, способны установить расстояние до эпицентра.

Разберем теперь другой практический вопрос — изгибание балки, стержня или бруска. Чему равны силы, необходимые для изгибания балки произвольного поперечного сечения? Мы определим эти силы для балки круглого сечения, но ответ будет пригоден для балки любой формы. Чтобы сберечь время, мы кое-где упростим дело, так что теория, которую мы разовьем, будет только приближенной. Наши результаты верны лишь при том условии, что радиус изгибания много больше толщины балки.

Представьте, что вы ухватились за оба конца прямой балки и согнули ее в виде кривой, похожей на ту, что изображена на фиг. 38.11.

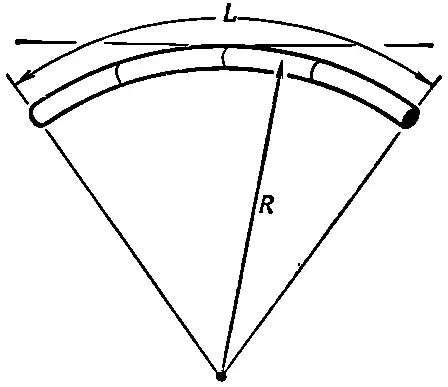
Фиг. 38.11. Изогнутая балка.

Что же происходит внутри балки? Раз она искривлена, значит, материал на внутренней стороне сгиба сжат, а на внешней стороне растянут. Но имеется какая-то поверхность, более или менее параллельная оси балки, которая и не сжата, и не растянута. Называется она нейтральной поверхностью. По-видимому, эта поверхность проходит где-то «посредине» поперечного сечения. Можно показать (но я не буду этого здесь делать), что для небольшого изгиба простой балки нейтральная поверхность проходит через «центр тяжести» поперечного сечения. Но это справедливо только для «чистого» сгиба, т. е. когда балка не растягивается и не сжимается как целое.

При чистом сгибе тонкий поперечный отрезок балки возмущен (фиг. 38.12, а).

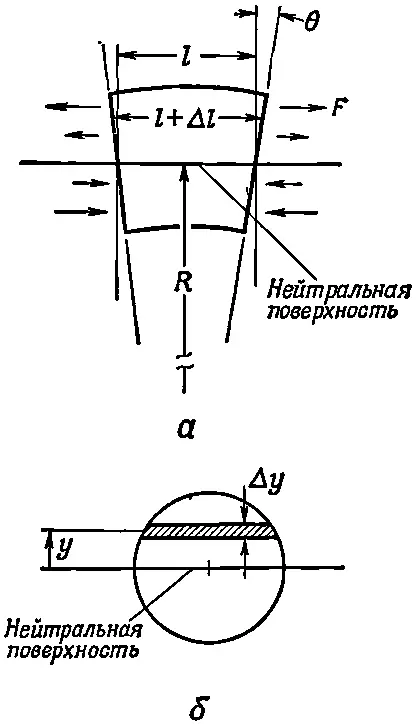
Фиг. 38.12. Маленький отрезок изогнутой балки (а) и поперечное сечение балки (б).

Материал под нейтральной поверхностью испытывает деформацию сжатия, которая пропорциональна расстоянию от нейтральной поверхности, а материал над ней растянут тоже пропорционально расстоянию от нейтральной поверхности. Таким образом, продольное удлинение Δ l пропорционально высоте у . Константа пропорциональности равна просто длине l , деленной на радиус кривизны балки (см. фиг. 38.12):

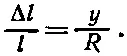
Так что напряжение, т. е. сила, действующая на единичную площадь в некоторой маленькой полоске вблизи у , тоже пропорциональна расстоянию от нейтральной поверхности

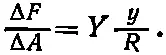(38.34)

Теперь рассмотрим те силы , которые привели бы к подобной деформации. Силы, действующие на маленький отрезок, изображенный на фиг. 38.12, показаны на том же рисунке. Если мы возьмем любое поперечное сечение, то действующие на нем силы направлены в одну сторону выше нейтральной поверхности и в другую — ниже ее. Получается пара сил, которая создает «изгибающий момент» M, под которым мы понимаем момент силы относительно нейтральной линии. Интегрируя произведение силы на расстояние от нейтральной поверхности, можно вычислить полный момент на одной из граней отрезка фиг. 38.12:

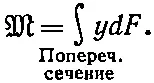(38.35)

Согласно (38.34), dF = Y ( y / R ) dA , так что

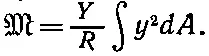
Но интеграл от y 2 dA можно назвать «моментом инерции» геометрического поперечного сечения относительно горизонтальной оси, проходящей через его «центр масс» [53] Это и есть момент инерции пластинки единичной плотности и с единичной площадью сечения ; мы будем обозначать его через I , т. е.

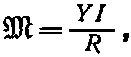(38.36)

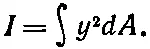(38.37)

Уравнение (38.36) дает нам соотношение между изгибающим моментом M и кривизной балки 1/R. «Жесткость» балки пропорциональна Y и моменту инерции I . Другими словами, если вы хотите какую-то балку, скажем из алюминия, сделать как можно жестче, то вы должны как можно больше вещества поместить как можно дальше от оси, относительно которой берется момент инерции. Но этого нельзя доводить до предела, ибо тогда балка не будет искривляться так, как мы предположили: она согнется или скрутится и снова станет слабее. Вот почему каркасные балки делают в форме буквы I или Н (фиг. 38.13).

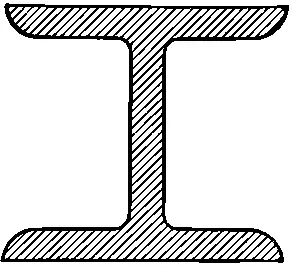
Фиг. 38.13. Двутавровая балка.

В качестве примера применения нашего уравнения (38.36) для балки вычислим отклонение консольной балки под действием сосредоточенной силы W, действующей на ее свободный конец (фиг. 38.14).

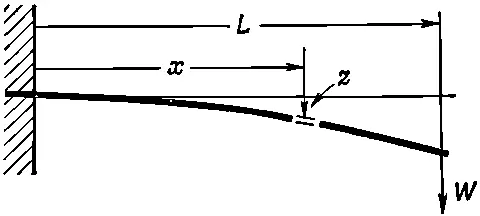
Фиг. 38.14. Консольная балка с нагрузкой на конце.

(Консольная балка закреплена одним концом, который вмурован в стенку.) Какая же тогда будет форма балки? Обозначим отклонение на расстоянии х от закрепленного конца через z; мы хотим найти z ( x ). Будем вычислять только малые отклонения. Как вы знаете из курса математики, кривизна 1/R любой кривой z ( x ) задается выражением

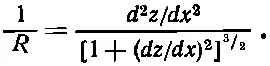(38.38)

Нас интересуют только малые изгибы (обычная вещь в инженерных конструкциях), поэтому квадратом производной ( dz / dx ) 2можно пренебречь по сравнению с единицей и считать