Ричард Фейнман - Том 2. Электромагнетизм и материя
- Название:Том 2. Электромагнетизм и материя
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:неизвестен
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Ричард Фейнман - Том 2. Электромагнетизм и материя краткое содержание
Том 2. Электромагнетизм и материя - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:

Фиг. 38.17. Координаты кривой продольно изогнутой балки S и θ.
Тогда кривизна будет равна скорости изменения угла с расстоянием
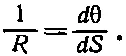
Поэтому точное уравнение (38.44) можно записать в виде
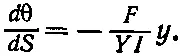
После взятия производной этого уравнения по S и замены dy / dS на sinθ получим
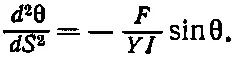 (38.47)
(38.47)
[Если углы θ малы, то мы снова приходим к уравнению (38.45), стало быть здесь все в порядке].
Не знаю, можете ли вы еще удивляться, но уравнение (38.47) получилось в точности таким же, как и для колебаний маятника с большой амплитудой (разумеется, с заменой F / YI другой постоянной). Еще раньше, в гл. 9 (вып. 1), мы узнали, как находить решение такого уравнения численным методом [55] Решение его можно выразить также через особые функции, называемые «эллиптическими функциями Якоби», которые когда-то раз навсегда были вычислены и протабулированы.
. В ответе вы получите очаровательную кривую. На фиг. 38.18 показаны три кривые для разных значений постоянной F / YI .
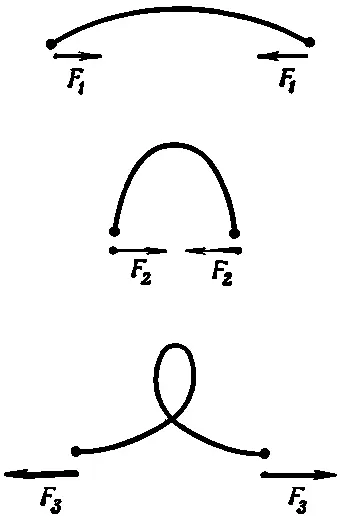
Фиг. 38.18. Формы продольно изогнутого стержня.
Глава 39 УПРУГИЕ МАТЕРИАЛЫ [56] Литература: Ch. Kittel, Introduction to Solid State Physics, 2nd ed., New York, 1956. (Имеется перевод: Ч. Киттель, Введение в физику твердого тела, Физматгиз, М., 1962.)
§ 1. Тензор деформации
В предыдущей главе мы говорили о возмущениях упругих тел в простых случаях. В этой главе мы посмотрим, что может происходить внутри упругого материала в общем случае . Как описать условия напряжения и деформации в большом куске желе, скрученном и сжатом каким-то очень сложным образом? Для этого необходимо описать локальную деформацию в каждой точке упругого тела, а это можно сделать, задав в ней набор шести чисел — компонент симметричного тензора. Ранее (в гл. 31) мы говорили о тензоре напряжений, теперь же нам потребуется тензор деформации.
Предположим, что мы взяли недеформированный материал и, прикладывая напряжение, наблюдаем за движением маленького пятнышка примеси, попавшей внутрь. Пятнышко, которое вначале находилось в точке Р и имело положение r=(x, у , z), передвигается в новую точку Р ', т. е. в положение r'=( х ', у ', z'), как это показано на фиг. 39.1.
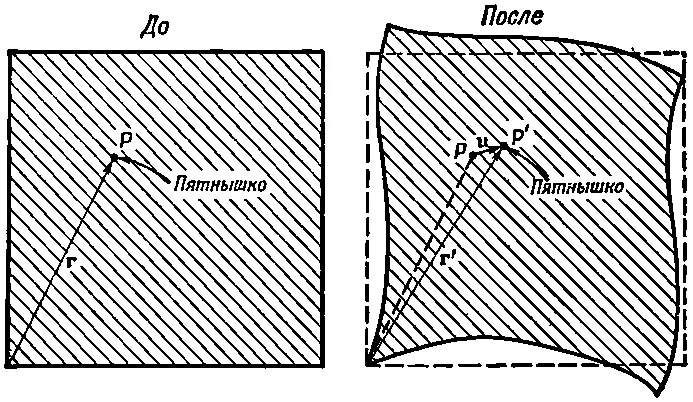
Фиг. 39.1. Пятнышко примеси в материале из точки Р недеформированного кубика после деформации перемещается в точку Р'.
Мы будем обозначать через uвектор перемещения из точки Р в точку Р ', т. е.
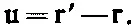 (39.1)
(39.1)
Перемещение uзависит, конечно, от точки Р , из которой оно выходит так, что и есть векторная функция от rили от ( х, у, z ).
Сначала рассмотрим простейший случай, когда деформация по всему материалу постоянна, т. е. то, что называется однородной деформацией . Предположим, например, что мы взяли балку из какого-то материала и равномерно ее растянули. Иначе говоря, мы просто равномерно изменили ее размер в одном направлении, скажем в направлении оси х (фиг. 39.2).
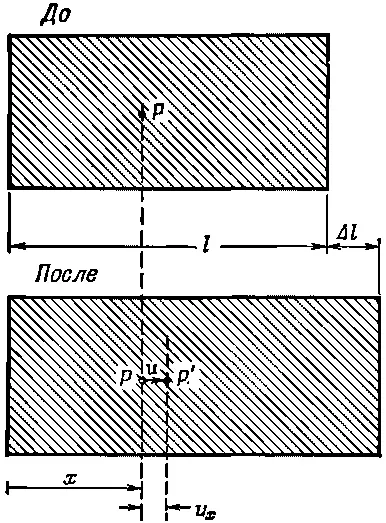
Фиг. 39.2. Однородная деформация растяжения.
Перемещение u x пятнышка с координатой х пропорционально самому х .
Действительно,
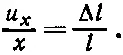
Мы будем записывать u x следующим образом:
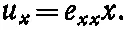
Разумеется, константа пропорциональности е хх — это то же, что наше старое отношение Δ l / l . (Скоро вы увидите, почему нам потребовался двойной индекс.)
Если же деформация неоднородна, то связь между х и u x в материале будет изменяться от точки к точке. В таком общем случае мы определим е хх как своего рода локальную величину Δ l / l , т. е.
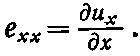 (39.2)
(39.2)
Это число, которое теперь будет функцией х, у и z , описывает величину растяжения в направлении оси х по всему куску желе. Возможны, конечно, растяжения и в направлении осей у и z . Мы будем описывать их величинами
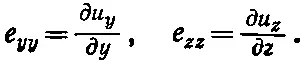 (39.3)
(39.3)
Кроме того, нам нужно описать деформации типа сдвигов. Вообразите, что в первоначально невозмущенном желе вы выделили маленький кубик. Нажав на желе, мы изменяем его форму, и наш кубик может превратиться в параллелограмм (фиг. 39.3) [57] Предположим на минуту, что полный угол сдвига θ делится на две равные части, чтобы деформация была симметричной относительно осей x и y.
.
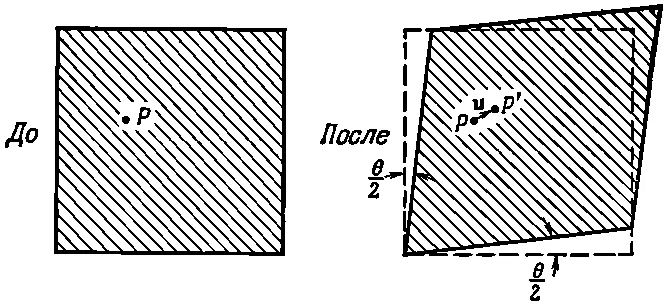
Фиг. 39.3. Однородная деформация сдвига.
При такой деформации перемещение в направлении х каждой частицы пропорционально ее координате у :
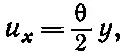 (39.4)
(39.4)
а перемещение в направлении у пропорционально х :
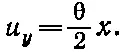 (39.5)
(39.5)
Таким образом, деформацию сдвигового типа можно описать с помощью

где
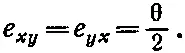
Интервал:
Закладка:






