Ричард Фейнман - Том 2. Электромагнетизм и материя

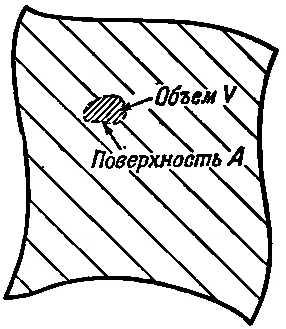
Фиг. 39.5. Маленький элемент объема V, ограниченный поверхностью А,

Если этот кусочек находится в равновесии, то полная действующая на него сила Fдолжна быть равна нулю. Можно считать, что эта сила состоит из двух частей, одна из которых обусловлена «внешними» силами, подобными гравитации, действующими на расстоянии на вещество нашего кусочка и приводящими к величине силы на единицу объема f внешн. Полная же внешняя сила F внешнравна интегралу от f внешнпо всему объему кусочка:

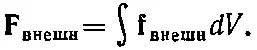(39.23)

В равновесии эти силы балансируются полной силой F внутр, действующей по поверхности А со стороны окружающего материала. Когда же этот кусочек не находится в равновесии, а движется, сумма внутренних и внешних сил будет равна произведению массы на ускорение. При этом мы получаем

(39.24)

где ρ—плотность материала, а .. r— его ускорение. Теперь мы можем скомбинировать уравнения (39.23) и (39.24) и написать

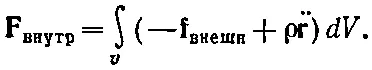(39.25)

Нашу запись можно упростить, положив

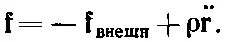(39.26)

Тогда уравнение (39.25) запишется в виде

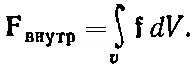(39.27)

Величина, названная нами F внутр, связана с напряжениями в материале. Тензор напряжений S ij был определен нами в гл. 31 таким образом, что x-компонента силы dF , действующей на элемент поверхности da с нормалью n, задается выражением

(39.28)

Отсюда х-компонента силы F внутр, действующей на наш кусочек, равна интегралу от dF x по всей поверхности. Подставляя это в x-компоненту уравнения (39.27), получаем

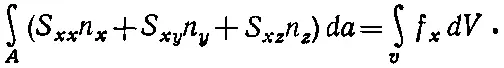(39.29)

Оказалось, что поверхностный интеграл связан с интегралом по объему, а это напоминает нам нечто знакомое по главам об электричестве. Заметьте, что если не обращать внимания на первый значок х в каждом из S в левой части (39.29), то она выглядит в точности как интеграл от величины ( S· n), т.е. нормальной компоненты вектора по поверхности. Она была бы равна потоку Sчерез объем. А используя теорему Гаусса, поток можно было бы записать в виде объемного интеграла от дивергенции S. На самом деле все это справедливо независимо от того, есть ли у нас индекс х или нет. Это просто математическая теорема, которая доказывается интегрированием по частям. Другими словами, уравнение (39.29) можно превратить в

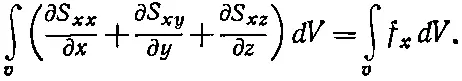(39.30)

Теперь можно отбросить интегралы по объему и написать дифференциальное уравнение для любой компоненты f:

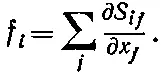(39.31)

Оно говорит нам, как связана сила, действующая на единицу объема с тензором напряжения S ij .

Вот как работает эта теория внутренних движений твердого тела. Если первоначально нам известны перемещения, задаваемые, скажем, вектором u, то можно найти деформации e ij . Из деформаций с помощью уравнения (39.12) можно получить напряжения. Затем с помощью уравнения (39.31) мы из напряжений можем найти плотности сил f. А зная f, мы из уравнения (39.26) получаем ускорение .. rв материале, которое подскажет нам, как изменятся перемещения. Собирая все это вместе, мы получаем ужасно сложные уравнения движения упругого твердого тела. Я просто напишу вам ответ для изотропного материала. Если вы воспользуетесь для S ij уравнением (39.20) и запишете e ij в виде 1/ 2(∂ u i /∂ x j +∂ u j /∂ x i ), то окончательно получите векторное уравнение:

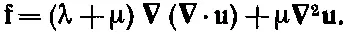(39.32)

Вы можете очень просто убедиться в том, что уравнение должно иметь такую форму. Сила должна зависеть от второй производной — перемещения u. Но какие можно составить вторые производные uтак, чтобы они были векторами? Одна из них ∇( ∇· u); это самый настоящий вектор. Есть еще только одна такая комбинация — это ∇ 2 u. Так что наиболее общей формой силы будет

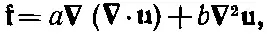
что как раз дает (39.32) с другим определением постоянных. Вас может удивить, почему у нас нет третьего слагаемого ∇× ∇× u, которое тоже вектор. Но вспомните, что ∇× ∇× uв точности равно ∇ 2 u- ∇( ∇· u), т. е. это линейная комбинация двух уже написанных слагаемых. Так что оно не добавит ничего нового. Мы еще раз доказали, что в изотропном материале есть только две упругие постоянные.

Для получения уравнения движения материала мы можем положить выражение (39.32) равным ρ∂ 2 u/∂ t 2и, пренебрегая объемными силами типа силы тяжести, написать

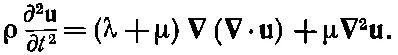(39.33)

Это уравнение выглядит похожим на волновое уравнение, с которым мы познакомились в электромагнетизме, за исключением одного добавленного слагаемого, которое усложняет дело. Для материалов, упругие свойства которых всюду одинаковы, мы можем увидеть, на что похоже общее решение. Вы, наверное, помните, что любое векторное поле может быть записано в виде суммы двух векторов, у одного из которых нулю равна дивергенция, а у другого — ротор. Другими словами, можно положить