Ричард Фейнман - Том 2. Электромагнетизм и материя

Есть и другие материалы, которые ведут себя очень странным и сложным образом. Чем сложнее материал, тем причудливей его поведение. Если мы возьмем лист сарана [58] Пластик с мудреным названием «поливинилиденхлорид», применяемый для обертки.— Прим. ред. , скомкаем его и бросим на стол, то постепенно он расправится и примет свою первоначальную плоскую форму. На первый взгляд кажется соблазнительным считать, что здесь основную роль играет именно упругость. Но простой подсчет покажет, что она слишком слаба (на несколько порядков слабее), чтобы как-то влиять на этот эффект. Оказывается, что здесь соревнуются два механизма: «нечто» внутри материала «помнит» первоначальную форму и «пытается» вернуться к старому виду, а «нечто» другое «предпочитает» новую форму и сопротивляется возврату к старой.

Я не хочу вдаваться в подробности и описывать тот механизм, который играет роль в поведении скомканного листа сарана, но получить представление о том, как такие эффекты происходят, вы можете на следующей модели . Представьте себе материал, изготовленный из длинных гибких, но крепких нитей вперемешку с пустотелыми ячейками, заполненными вязкой жидкостью. Представьте также, что между каждой ячейкой и соседними с ней имеются узкие проходы, по которым жидкость может медленно проникать из одной ячейки в другую. Если мы скомкаем лист такого материала, то длинные нити деформируются, жидкость из одной ячейки будет выжиматься и переходить в другие ячейки, которые оказались растянутыми. Когда же мы отпускаем лист, то длинные нити будут стремиться вернуться к своей первоначальной форме. Однако, чтобы сделать это, они должны заставить жидкость возвратиться на свое прежнее место, что происходит довольно медленно из-за ее вязкости. Силы, которые мы прилагаем, комкая лист, гораздо больше сил, развиваемых нитями. Скомкать лист можно очень быстро, а вот вернуться к прежнему виду он сможет гораздо медленнее. Несомненно, что здесь основную роль играет комбинация больших, жестких молекул и более мелких, но более подвижных. Этот механизм согласуется также с тем фактом, что материал быстрее принимает свою первоначальную форму, если он нагрет, и медленнее в холодном состоянии: тепло увеличивает подвижность (уменьшает вязкость) мелких молекул.

Хотя мы обсуждали, как происходит нарушение закона Гука, но, по-видимому, наиболее удивительно все же не нарушение этого закона при больших деформациях, а его универсальность. Некоторое понятие о том, почему так происходит, вы можете получить, рассматривая энергию деформации материала. Утверждение о том, что напряжение пропорционально деформации, равносильно утверждению, что энергия деформации изменяется как квадрат напряжения. Предположим, что мы скрутили стержень на малый угол θ. Если справедлив закон Гука, то энергия деформации должна быть пропорциональна квадрату θ. Предположим, что энергия является некоторой произвольной функцией угла. Мы можем записать ее в виде разложения Тэйлора около нуля:

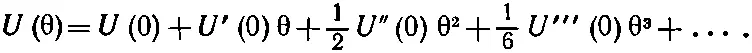(39.40)

Момент силы τ представляет производную U по углу, поэтому

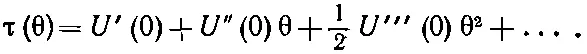(39.41)

Если теперь отсчитывать угол от положения равновесия , то первое слагаемое будет равно нулю. Таким образом, первое оставшееся слагаемое пропорционально θ и при достаточно малых углах оно будет превосходить слагаемое с θ 2. [На самом деле, внутренне материалы в достаточной мере симметричны, так что τ(θ)=-τ(-θ); слагаемое с θ 2оказывается нулем, а отклонение от линейности происходит только из-за слагаемого с θ 3. Однако нет причин, по которым это было бы верно для растяжения и сжатия.] Единственно, что мы не объяснили, — почему материалы обычно разрушаются вскоре после того, как становятся существенными члены высшего порядка.

Последний вопрос в теории упругости, который я разберу, — это попытка вычислить упругие постоянные материала, исходя из некоторых свойств атомов, составляющих этот материал. Мы рассмотрим простой случай ионного кубического кристалла типа хлористого натрия. Размер или форма деформированного кристалла изменяются. Такие изменения приводят к увеличению потенциальной энергии кристалла. Для вычисления изменения энергии деформации следует знать, куда идет каждый атом. Чтобы сделать полную энергию как можно меньше, атомы в решетке сложных кристаллов перегруппировываются весьма сложным образом. Это довольно сильно затрудняет вычисление энергии деформации. Но понять, что получается в случае простого кубического кристалла, все-таки можно. Возмущения внутри кристалла будут геометрически подобны возмущениям его внешних граней.

Упругие постоянные кубического кристалла можно вычислить следующим образом. Прежде всего мы предположим наличие некоего закона взаимодействия между каждой парой атомов в кристалле. Затем вычислим изменение внутренней энергии кристалла при отклонении от равновесной формы. Это даст нам соотношения между энергией и деформацией, которая квадратична по деформациям. Сравнивая энергию, полученную таким способом, с уравнением (39.13), можно идентифицировать коэффициенты при каждом слагаемом с упругими постоянными C ijkl .

В нашем примере мы будем предполагать следующий простой закон взаимодействия: между соседними атомами действуют центральные силы, имея в виду, что они действуют по линии, соединяющей два соседних атома. Мы ожидаем, что силы в ионных кристаллах должны быть именно такого типа, ибо в основе их лежит простое кулоновское взаимодействие. (При ковалентной связи силы обычно более сложны, ибо они приводят и к боковому давлению на соседние атомы; но нам все эти усложнения ни к чему.) Кроме того, мы собираемся учесть только силу взаимодействия каждого атома с ближайшим к нему и следующими поблизости соседями. Другими словами, мы будем делать приближение, в котором пренебрежем силами между далекими атомами. На фиг. 39.10,а показаны силы в плоскости ху , которые мы будем учитывать. Следует еще учесть соответствующие силы в плоскостях yz и zx .

Поскольку нас интересуют только упругие постоянные, которые описывают малые деформации, и, следовательно, в выражении для энергии нам нужны только слагаемые, квадратичные по деформациям, то можно считать, что силы между каждой парой атомов изменяются с перемещением линейно.