Ричард Фейнман - Том 2. Электромагнетизм и материя

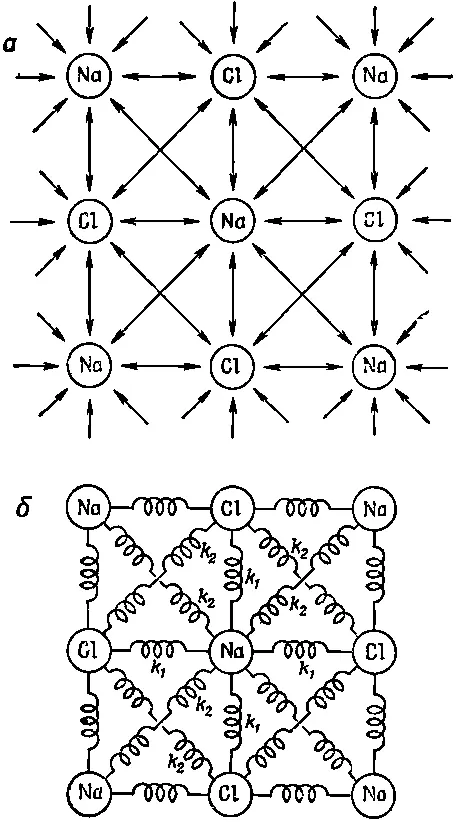
Фиг. 39.10. Принимаемые нами в расчет межатомные силы (а) и модель, в которой атомы связаны пружинками (б).

Поэтому для наглядности можно представлять, что каждая пара атомов соединена «линейной» пружинкой (фиг. 39.10, б). Все пружинки между атомами натрия и хлора должны иметь одну и ту же упругую постоянную, скажем k 1. Пружинки между двумя атомами натрия и двумя атомами хлора могут иметь различные постоянные, но я хочу упростить наши рассуждения, и поэтому буду считать эти постоянные равными. Обозначим их через k 2. (Позднее, когда мы посмотрим, как пойдут вычисления, вы сможете вернуться назад и сделать их разными.)

Предположим теперь, что кристалл возмущен однородной деформацией, описываемой тензором e ij . В общем случае у него будут компоненты, содержащие х, у и z, но мы для большей наглядности рассмотрим только деформации с тремя компонентами: е хх , е xy и е yy . Если один из атомов выбрать в качестве начала координат, то перемещение любого другого атома задается уравнением типа (39.9):

(39.42)

Назовем атом с координатами х = у =0 «атомом 1», а номера его соседей показаны на фиг. 39.11.

Фиг , 39.11. Перемещение ближайших и следующих поблизости соседей атома 1. ( Масштаб сильно искажен .)

Обозначая постоянную решетки через а , мы получаем х - и y-компоненты перемещения u x , u y , выписанные в табл. 39.1.

Таблица 39.1. КОМПОНЕНТЫ ПЕРЕМЕЩЕНИЯ u x, u у

Теперь можно вычислить энергию, запасенную в пружинках, которая равна произведению k 2/2 на квадрат растяжения каждой пружинки. Так, энергия горизонтальной пружинки между атомами 1 и 2 будет равна

(39.43)

Заметьте, что с точностью до первого порядка y -перемещение атома 2 не изменяет длины пружинки между атомами 1 и 2. Однако, чтобы получить энергию деформации диагональной пружинки, той, что идет к атому 3, нам нужно вычислить изменение длины как из-за вертикального, так и из-за горизонтального перемещений. Для малых отклонений от начала координат куба изменение расстояния до атома 3 можно записать в виде суммы компонент u х и u v в диагональном направлении:

Воспользовавшись величинами u х и u y . можно получить выражение для энергии

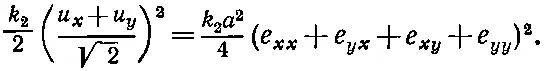(39.44)

Для полной энергии всех пружинок в плоскости ху нам нужна сумма восьми членов типа (39.43) и (39.44). Обозначая эту энергию через U 0, получаем

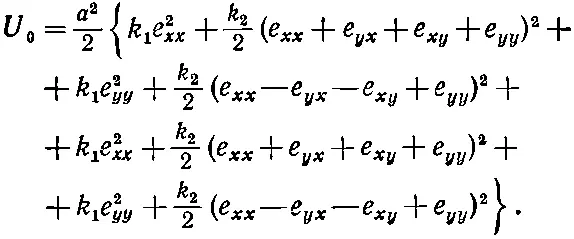(39.45)

Чтобы найти полную энергию всех пружинок, связанных с атомом 1, мы должны сделать некую добавку к уравнению (39.45). Хотя нам нужны только х - и y-компоненты деформации, вклад в них дает еще некоторая добавочная энергия, связанная с диагональными соседями вне плоскости ху . Эта добавочная энергия равна

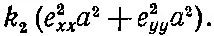(39.46)

Упругие постоянные связаны с плотностью энергии w уравнением (39.13). Энергия, которую мы вычислили, связана с одним атомом, точнее это удвоенная энергия, приходящаяся на один атом, ибо на каждый из двух атомов, соединенных пружинкой, должно приходиться по 1/ 2ее энергии. Поскольку в единице объема находится 1/a 3атомов, то w и U 0связаны соотношением

Чтобы найти упругие постоянные C ijkl , нужно только возвести в квадрат суммы в скобках в уравнении (39.45), прибавить (39.46) и сравнить коэффициенты при е ij е kl с соответствующими коэффициентами в уравнении (39.13). Например, собирая слагаемые с е 2 xx и е 2 yy, мы находим, что множитель при нем равен

поэтому

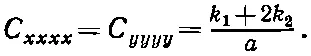
В остальных слагаемых нам встретится небольшое усложнение. Поскольку мы не можем отличить произведения е хх е yy от е yy е хх , то коэффициент при нем в выражении для энергии равен сумме двух членов в уравнении (39.13). Коэффициент при е хх е yy в уравнении (39.45) равен 2k 2, так что получаем

Однако из-за симметрии выражения для энергии при перестановке двух первых значений с двумя последними можно считать, что С кхуу = С уухх , поэтому

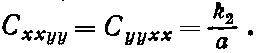
Таким же способом можно получить

Заметьте, наконец, что любой член, содержащий один раз значок х или у , равен нулю, как это было найдено ранее из соображений симметрии. Подытожим наши результаты:

(39.47)

Итак, оказалось, что мы способны связать макроскопические упругие постоянные с атомными свойствами, которые проявляются в постоянных k 1и k 2. В нашем частном случае C хуxу = C ххуу .Эти члены для кубического кристалла, как вы, вероятно, заметили из хода вычислений, оказываются всегда равными, какие бы силы мы ни принимали во внимание, но только при условии , что силы действуют вдоль линии, соединяющей каждую пару атомов, т. е. до тех пор, пока силы между атомами подобны пружинкам и не имеют боковой составляющей (которая несомненно существует при ковалентной связи).