Ричард Фейнман - Том 2. Электромагнетизм и материя

Если мы отбросим f вязк, то в уравнении (40.4) все нам известно, за исключением выражения для ускорения. Может показаться, что формула для ускорения частиц жидкости должна быть очень простой, ибо очевидно, что если v— скорость частицы в некотором месте жидкости, то ускорение ее будет просто равно ∂ v /∂ t . Но это совсем неверно , и по довольно хитрой причине. Производная ∂ v /∂ t выражает изменение скорости v( х, у, z, t ) в фиксированной точке пространства. А нам нужно знать, как изменяется скорость данной капельки жидкости. Представьте, что мы пометили одну капельку воды цветной краской и можем наблюдать за ней. За маленький интервал времени Δ t эта капелька продвинется в другое положение. Если капелька движется по некоторому пути, изображенному на фиг. 40.4, то за промежуток Δ t она из точки Р 1переместится в точку Р 2.

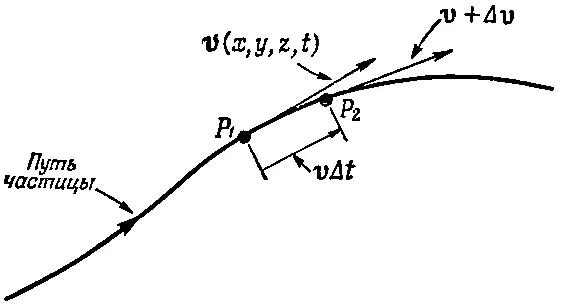
Фиг. 40.4. Ускорение частицы жидкости.

Фактически в направлении оси х она передвинется на расстояние v x Δ t , в направлении оси у — на расстояние v у Δ t , а в направлении оси z — на расстояние v z Δ t . Мы видим, что если v( х, у, z, t ) — скорость частицы в момент t , то скорость той же самой частицы в момент t +Δ t представляет величину v ( х +Δx, у +Δ y , z+Δz, t +Δ t ), причем

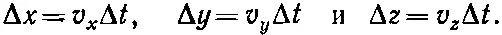
Из определения частных производных [вспомните уравнения гл. 2, вып. 5] мы с точностью до членов первого порядка получаем

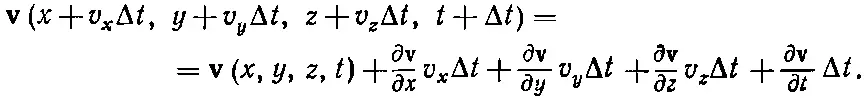
Ускорение же Δ v /Δ t будет равно

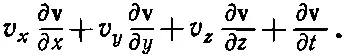
Считая ∇вектором, это можно записать символически:

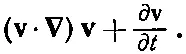(40.5)

Обратите внимание, что, даже когда ∂ v /∂ t =0, т. е. когда скорость в данной точке не изменяется, ускорение все же останется. Примером может служить вода, текущая с постоянной скоростью по кругу: она ускоряется даже тогда, когда скорость в данной точке не изменяется. Причина, разумеется, состоит в том, что скорость данной капельки воды, которая первоначально находилась в одной точке, моментом позднее будет иметь другое направление — это центростремительное ускорение.

Остальная часть нашей теории — чисто математическая: нахождение решения уравнения движения, полученного подстановкой ускорения (40.5) в (40.4), т. е.

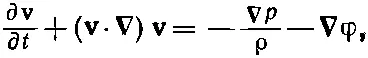(40.6)

где слагаемое с вязкостью уже выброшено. Воспользовавшись известным тождеством из векторного анализа, это уравнение можно переписать по-другому:

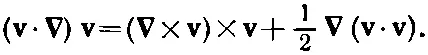
Если определить новое векторное поле Ωкак ротор скорости v, т. е.

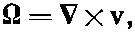(40.7)

то векторное тождество можно записать так:

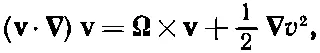
а наше уравнение движения (40.6) примет вид

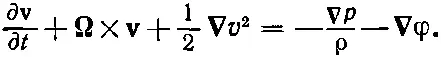(40.8)

Вы можете проверить эквивалентность уравнений (40.6) и (40.8), расписывая их по компонентам и сравнивая их, воспользовавшись при этом выражением (40.7).

Если Ωвсюду равно нулю, то такой поток мы называем безвихревым (или потенциальным). В гл. 3, § 5 (вып. 5), мы уже определяли величину, называемую циркуляцией векторного поля. Циркуляция по любой замкнутой петле в жидкости равна криволинейному интегралу от скорости жидкости в данный момент времени вокруг этой петли:

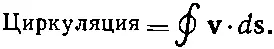
Циркуляция на единицу площади для бесконечно малой петли по теореме Стокса будет тогда равна ∇× v. Таким образом, Ωпредставляет собой циркуляцию вокруг единичной площади (перпендикулярной направлению Ω). Кроме того, ясно, что если в любое место жидкости поместить маленькую соринку (именно соринку, а не бесконечно малую точку), то она будет вращаться с угловой скоростью Ω/2. Попытайтесь доказать это. Вы можете также попробовать доказать, что для ведра воды на вращающемся столике Ωравна удвоенной локальной угловой скорости воды.

Если нас интересует только поле скоростей, то из наших уравнений можно исключить давление. Взяв ротор обеих частей уравнения (40.8) и вспомнив, что ρ — величина постоянная, а ротор любого градиента равен нулю, а также использовав уравнение (40.3), находим

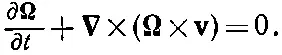(40.9)

Это уравнение вместе с уравнениями

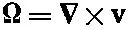(40.10)

и

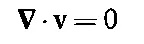(40.11)

полностью описывают поле скоростей v. На языке математики — если в некоторый момент мы знаем Ω,то мы знаем ротор вектора скорости и, кроме того, знаем, что его дивергенция равна нулю, так что в этих физических условиях у нас есть все необходимое для определения скорости vповсюду. (Все это в точности напоминает нам знакомые условия в магнетизме, где ∇·B=0 и ∇× B= j/ε 0c 2.) Таким образом, данная величина Ωопределяет vточно так же, как jопределяет В. Затем из известного значения vуравнение (40.9) даст нам скорость изменения Ω, откуда мы можем получить новую Ωв следующий момент. Используя снова уравнение (40.10), найдем новое значение vи т. д. Теперь вы видите, как в эти уравнения входит весь механизм, необходимый для вычисления потока. Заметьте, однако, что эта процедура дает только скорости, а всю информацию о давлении мы потеряли.