Ричард Фейнман - Том 2. Электромагнетизм и материя

Отметим особое следствие нашего уравнения. Если в какой-то момент времени t повсеместно Ω=0, то ∂ Ω/∂ t тоже исчезает, так что Ωвсюду останется равной нулю и в момент t +Δt. Отсюда следует, что поток все время остается безвихревым. Если вначале поток не вращался, то он так никогда и не начнет вращаться. При этом уравнения, которые мы должны решать, таковы:

Они в точности напоминают уравнения электростатики или магнитостатики в пустом пространстве. Позднее мы вернемся к ним и рассмотрим некоторые частные задачи.

Вернемся к уравнениям движения (40.8), но ограничимся теперь приближением «стационарного» потока. Под стационарным потоком я подразумеваю поток, скорость которого в любом месте жидкости никогда не изменяется. Жидкость в любой точке постоянно заменяется новой жидкостью, движущейся в точности таким же образом. Картина скоростей всегда выглядит одинаково, т. е. vпредставляет статическое векторное поле. Как в магнитостатике мы рисовали силовые линии, так и здесь можно начертить линии, которые всегда касательны к скорости жидкости (фиг. 40.5).

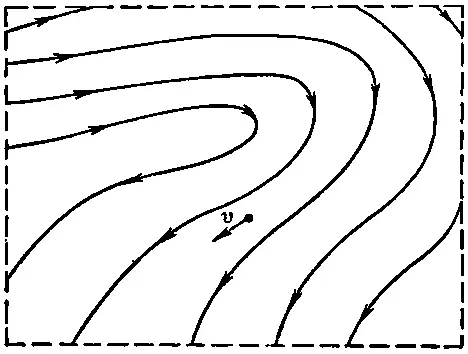
Фиг. 40.5. Линии тока стационарного потока.

Эти линии называются «линиями тока». Для стационарного потока они действительно представляют реальные пути частиц жидкости. (В нестационарном потоке картина линий тока меняется со временем, однако в любой момент времени она не представляет пути частиц жидкости.)

Стационарность потока вовсе не означает, что ничего не происходит — частички жидкости движутся и изменяют свои скорости. Это означает только то, что ∂ v /∂ t =0. Если теперь мы скалярно умножим уравнение движения на v, то слагаемое v·( Ω× v) выпадет и у нас останется только

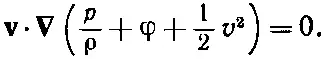(40.12)

Согласно этому уравнению, при малых перемещениях в направлении скорости жидкости величина внутри скобок не изменяется. В стационарном потоке все перемещения направлены вдоль линий тока; поэтому уравнение (40.12) говорит, что для всех точек вдоль линии тока

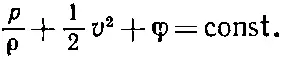(40.13)

Это и есть теорема Бернулли . Постоянная, вообще говоря, для различных линий тока может быть разной; мы знаем только, что левая часть уравнения (40.13) постоянна всюду вдоль данной линии тока . Заметьте, кстати, что если стационарный поток безвихревой, т. е. если для него Ω=0, то уравнение движения (40.8) дает нам соотношение

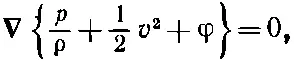
так что

(40.14)

Оно в точности напоминает уравнение (40.13), за исключением того, что теперь постоянная во всей жидкости одна и та же . На самом деле теорема Бернулли не означает ничего большего, чем утверждение о сохранении энергии. Подобные теоремы о сохранении дают нам массу информации о потоке без детального решения уравнений. Теорема Бернулли настолько важна и настолько проста, что мне бы хотелось показать вам, как можно ее получить другим способом, отличным от тех формальных вычислений, которые мы только что провели. Представьте себе пучок линий тока, образующих трубку тока (фиг. 40.6, а).

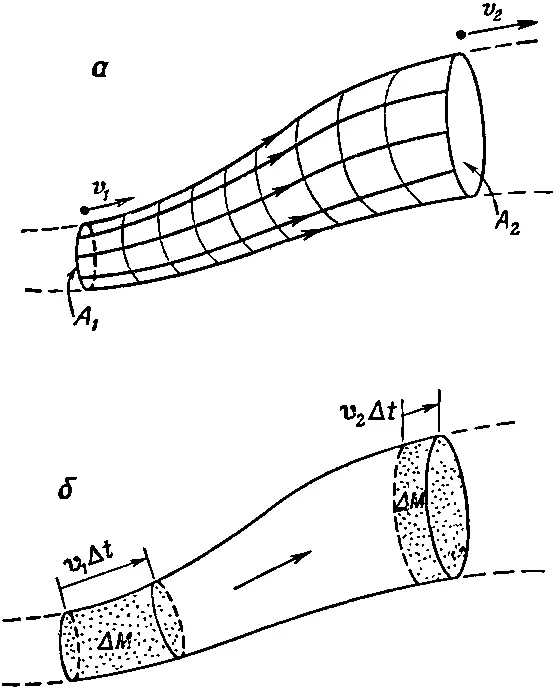
Фиг. 40.6. Движение жидкости в трубке.

Поскольку стенки трубки образуются линиями тока, то жидкость через них не протекает. Обозначим площадь на одном конце трубки через A 1, скорость жидкости через v 1, плотность через ρ 1, а потенциальную энергию через φ 1. Соответствующие величины на другом конце трубки мы обозначим через A 2, v 2, ρ 2и φ 2. После короткого интервала времени Δt жидкость на одном конце передвинется на расстояние v 1Δ t , а жидкость на другом конце — на расстояние v 2Δt (см. фиг. 40.6, б ). Сохранение массы требует, чтобы масса, которая вошла через A 1была равна массе, которая вышла через А 2. Изменение масс в этих двух концах должно быть одинаково:

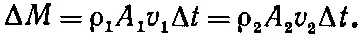
Таким образом, мы получаем равенство

(40.15)

Оно говорит нам, что при постоянном ρ скорость изменяется обратно пропорционально площади трубки тока.

Вычислим теперь работу, произведенную давлением в жидкости. Работа, произведенная над жидкостью, входящей со стороны сечения А 1, равна р 1A 1v 1АΔt, а работа, произведенная в сечении А 2, равна p 2 A 2 v 2Δ t . Следовательно, полная работа, произведенная над жидкостью, заключенной между A 1и А 2, будет

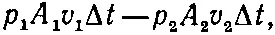
что должно быть равно возрастанию энергии массы жидкости ΔM при прохождении от А 1до А 2. Другими словами,

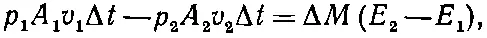(40.16)

где Е 1— энергия единицы массы жидкости в сечении А 1, а Е 2— энергия единицы массы в сечении А 2. Энергию единицы массы жидкости можно записать в виде

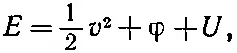
где 1/ 2 v 2— кинетическая энергия единицы массы, φ — потенциальная энергия, а U — дополнительный член, представляющий внутреннюю энергию единицы массы жидкости. Внутренняя энергия может соответствовать, например, тепловой энергии сжимаемой жидкости или химической энергии. Все эти величины могут изменяться от точки к точке. Воспользовавшись выражением для энергии в уравнении (40.16), получим