Ричард Фейнман - Том 2. Электромагнетизм и материя

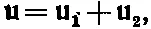(39.34)

где

(39.35)

Подставляя вместо uв уравнении (39.33) u 1+ u 2, получаем

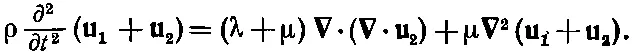(39.36)

Взяв дивергенцию этого уравнения, мы можем исключить из него u 1:

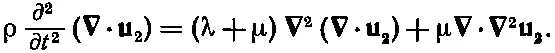
Поскольку операторы ∇ 2и ∇могут быть переставлены, можно вынести оператор дивергенции и получить

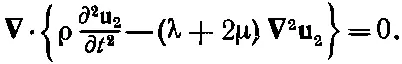(39.37)

А так как ∇× u 2, по определению, равно нулю, то ротор выражения в фигурных скобках также будет нулем, так что выражение в скобках само по себе тождественно равно нулю и

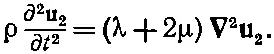(39.38)

Это векторное волновое уравнение для волн, движущихся со скоростью С 2=√(λ+2μ)/ρ. Поскольку ротор u 2есть нуль, то эти волны не связаны со сдвигом, а представляют просто волны сжатия наподобие звуковых, которые мы изучали в предыдущих главах и скорость которых как раз равна найденной нами для С прод.

Подобным же образом, беря ротор уравнения (39.36), можно показать, что u 1удовлетворяет уравнению

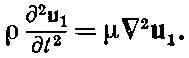(39.39)

Это снова векторное волновое уравнение для волн, распространяющихся со скоростью C 2=√μ/ρ. Поскольку ∇· u 1равно нулю, то перемещение u 1не приводит к изменению плотности; вектор u 1соответствует поперечным или сдвиговым волнам, которые встречались нам в предыдущей главе, а C 2=C сдвиг.

Если мы хотим знать статические напряжения в изотропном материале, то в принципе их можно найти, решая уравнение (39.32) с f, равным нулю (или равным статическим объемным силам, обусловленным силой тяжести, такой, как ρg) при определенных условиях, связанных с силами, действующими на поверхности нашего большого куска материала. Сделать это несколько сложнее, чем в соответствующих задачах электромагнетизма. Во-первых, это более трудно потому, что сами уравнения несколько сложнее, и, во-вторых, формы тех упругих тел, которыми мы обычно интересуемся, гораздо сложнее. На лекциях по электричеству мы часто интересовались решением уравнений Максвелла в областях сравнительно простой геометрической формы, таких, как цилиндр, сфера и т. д. В теории упругости, нам приходится заниматься объектами гораздо более сложной формы, например крюком подъемного крана, или коленчатым автомобильным валом, или ротором газовой турбины. Такие задачи иногда можно приближенно решить численным методом, воспользовавшись принципом минимальной энергии, о котором мы упомянули ранее. Другой способ — это воспользоваться моделями предметов и измерять внутренние напряжения экспериментально с помощью поляризованного света.

Метод этот состоит в следующем. Когда кусок упругого изотропного материала, например прозрачную пластмассу типа плексигласа, подвергают напряжению, в ней возникает двойное лучепреломление. Если пропускать через эту пластмассу поляризованный свет, то плоскость поляризации повернется на величину, связанную с напряжением. Измеряя угол плоскости поляризации, можно измерить напряжение. На фиг. 39.6 показан примерный вид этого устройства, а на фиг. 39.7 приведена фотография упругой модели сложной формы под напряжением.

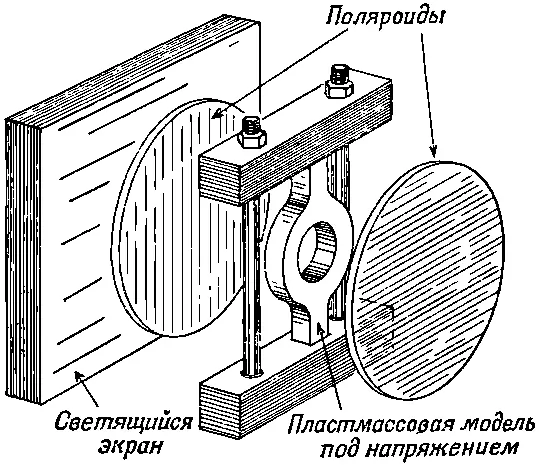
Фиг. 39.6. Измерение внутренних напряжений с помощью поляризованного света.

Фиг. 39.7. Вид напряженной пластмассовой модели между двумя скрещенными поляроидами.

Во всем, что до сих пор говорилось, мы предполагали, что напряжение пропорционально деформации, а это вообще-то неверно. На фиг. 39.8 приведена типичная диаграмма напряжение — деформация упругого материала.

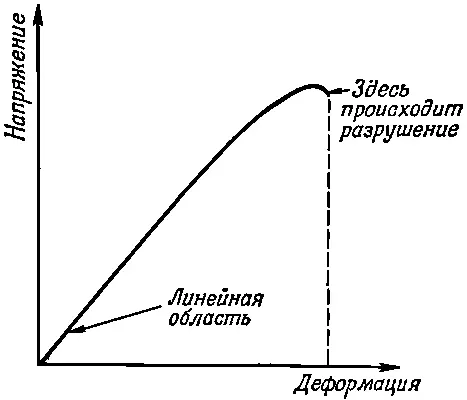
Фиг. 39.8. Типичная диаграмма напряжение — деформация для больших деформаций.

Для малых деформаций напряжение пропорционально деформации. Однако после некоторой точки зависимость напряжения от деформации начинает отклоняться от прямой линии. Для многих материалов, которые мы назовем «хрупкими», разрушение наступает, когда деформация несколько превысит ту точку, где кривая начинает загибаться. В общем же случае в диаграмме напряжение — деформация есть и другие усложнения. Например, когда вы деформируете предмет, существующие большие напряжения могут затем медленно уменьшиться со временем. Если вы достигнете высоких напряжений, однако ниже точки разрыва, а затем будете уменьшать деформацию, то напряжения будут возвращаться назад уже по другой кривой. Возникает небольшой гистерезисный эффект (наподобие того, что мы видели в связи между В и Н в магнитных материалах).

Напряжения, при которых происходит разрушение, сильно изменяются от материала к материалу. Некоторые материалы разрушаются при максимальном растягивающем напряжении. Другие же разрушаются при определенной величине напряжения сдвига . Скажем, мел гораздо слабее противостоит растяжению, чем сдвигу. Если вы потянете за концы палочки мела, то она сломается перпендикулярно направлению приложенной силы (фиг. 39.9, справа ).

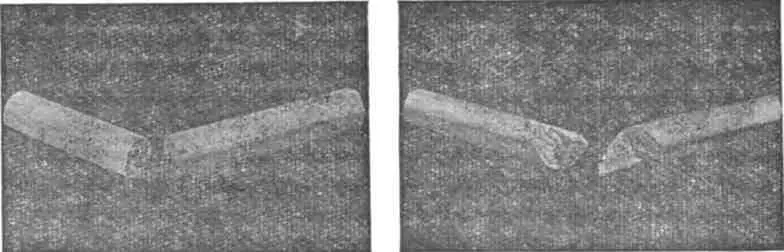
Фиг. 39.9. Сломанный кусочек мела: Справа — растягиванием за "концы", слева — скручиванием.

Ведь мел — это только спрессованные частички, которые легко растаскиваются в стороны, поэтому он ломается перпендикулярно приложенной силе. А в отношении сдвига этот материал гораздо крепче, так как в этом случае частицы мешают друг другу. Вспомните теперь, что когда мы скручиваем стержень, то в любом его поперечном сечении возникают сдвиги. Мы показали, кроме того, что сдвиг эквивалентен комбинации растяжения и сжатия под углом 45°. По этой причине при скручивании кусочек мела разломится по сложной поверхности, которая расположена под углом 45° к образующим. На фиг. 39.9 ( слева ) приведена фотография куска мела, сломанного таким способом. Мел ломается там, где напряжения максимальны.