Ричард Фейнман - Том 2. Электромагнетизм и материя

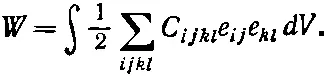(39.14)

Следовательно, это и есть потенциальная энергия, запасенная во внутренних напряжениях материала. Когда тело находится в равновесии, эта внутренняя энергия должна быть минимальной . Таким образом, проблема определения деформаций в теле может быть решена нахождением таких перемещений и по всему телу, при которых W минимальна. В гл. 19 (вып. 6) я говорил вам о некоторых общих идеях вариационного исчисления, применяемого при решении задач на минимизацию подобного рода. Однако сейчас мы больше не будем вдаваться в подробности этой задачи.

Сейчас нас главным образом будет интересовать то, что можно сказать относительно общих свойств тензора упругости. Прежде всего ясно, что на самом деле в C ijkl содержится не 81 различный параметр. Поскольку S ij и e ij — симметричные тензоры, каждый из которых включает только шесть различных элементов, то C ijkl состоит максимум из 36 различных компонент. Обычно же их гораздо меньше.

Рассмотрим специальный случай кубического кристалла. Плотность энергии w для него получается такой:

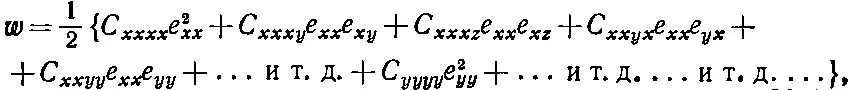(39.15)

т. е. всего 81 слагаемое! Но кубический кристалл обладает определенными симметриями. В частности, если кристалл повернуть на 90°, то все его физические свойства останутся теми же. Например, у него должна быть одна и та же жесткость относительно растяжения как в направлении оси у , так и в направлении оси х . Следовательно, если мы переменим наши определения осей координат х и у в уравнении (39.15), то энергия не должна измениться. Поэтому для кубического кристалла

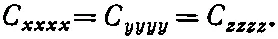(39.16)

Мы можем еще показать, что компоненты, наподобие С ххху , должны быть нулями. Кубический кристалл обладает тем свойством, что он симметричен при отражении относительно любой плоскости, перпендикулярной к одной из осей координат. Если мы заменим у на —y, то ничего не должно измениться. Но изменение у на - у меняет е xy на - е xy , так как перемещение в направлении + у будет теперь перемещением в направлении - у . Чтобы энергия при этом не менялась, С ххху должно переходить в - С ххху Но отраженный кристалл будет тем же, что и прежде, поэтому С ххxy должно быть таким же , как и - С ххху . Это может произойти только тогда, когда оба они равны нулю.

Но вы можете сказать: «Рассуждая таким же образом, можно сделать и C yyyy =0!» Это неверно. Ведь здесь у нас четыре игрека. Каждый у изменяет знак, а четыре минуса дают плюс. Если у встречается два или четыре раза, то такие компоненты не должны быть равны нулю. Нулю равны только те компоненты, у которых у встречается либо один , либо три раза. Таким образом, для кубического кристалла не равны нулю только те С , у которых один и тот же значок встречается четное число раз . (Рассуждения, которые мы провели для у , имеют силу и для х и для z.) Таким образом, выживают только компоненты типа С ххуу , С хуху , С хуух и т. д. Однако мы уже показали, что если изменить все х на у и наоборот (или все z на x и т. д.), то для кубического кристалла мы должны получить то же самое число. Это означает, что остаются всего три различные ненулевые возможности:

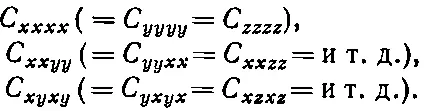(39.17)

Плотность же энергии для кубического кристалла выглядит так:

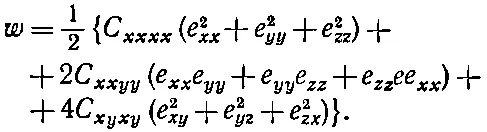(39.18)

У изотропного, т. е. некристаллического, материала симметрия еще выше. Числа С должны быть теми же самыми при любом выборе осей координат. При этом, как оказывается, существует другая связь между коэффициентами С :

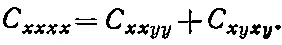(39.19)

Это можно усмотреть из следующих общих рассуждений. Тензор напряжений S ij должен быть связан с e ij способом, который совершенно не зависит от направления осей координат, т. е. он должен быть связан только с помощью скалярных величин. «Это очень просто», — скажете вы. «Единственный способ получить S ij из e ij — умножить последнее на скалярную постоянную. Получится как раз закон Гука: S ij =(Постоянная)×е ij». Однако это не совсем верно. Дополнительно здесь можно вставить единичный тензор δ ij , умноженный на некоторый скаляр, линейно связанный с е ij . Единственный инвариант, который можно составить и который линеен по е , — это ∑e ij . (Он преобразуется подобно х 2+ y 2+ z 2, а значит является скаляром.) Таким образом, наиболее общей формой уравнения, связывающего S ij с e ij для изотропного материала, будет

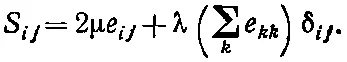(39.20)

(Первая константа обычно записывается как 2μ; при этом коэффициент μ равен модулю сдвига, определенному нами в предыдущей главе.) Постоянные μ, и λ называются упругими постоянными Лямэ . Сравнивая уравнения (39.20) с уравнением (39.12), вы видите, что

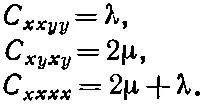(39.21)

Таким образом, мы доказали, что уравнение (39.19) действительно правильное. Вы видите также, что упругие свойства изотропного материала, как уже говорилось в предыдущей главе, полностью задаются двумя постоянными.

Коэффициенты С могут быть выражены через любые две из упругих постоянных, которые использовались ранее, например через модуль Юнга Y и отношение Пуассона σ. На вашу долю оставляю показать, что

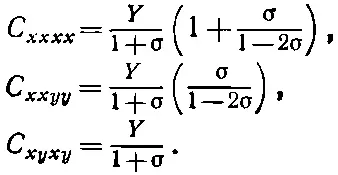(39.22)

Мы подчеркивали, что в упругом теле, находящемся в равновесии , внутренние напряжения распределяются так, чтобы энергия была минимальной. Посмотрим теперь, что происходит, если внутренние силы не уравновешены . Возьмем маленький кусочек материала внутри некоторой поверхности А (фиг. 39.5).