Ричард Фейнман - Том 2. Электромагнетизм и материя

Фиг. 38.7. Напряжение сдвига θ равно 2ΔD/D.

Из геометрии фигуры вы видите, что горизонтальный сдвиг δ верхнего края равен √2Δ D , так что

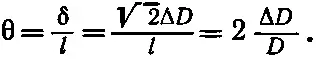(38.12)

Напряжение сдвига g определяется как отношение тангенциальной силы, действующей на грань, к площади грани g = G / A . Воспользовавшись уравнением (38.11), мы из (38.12) получаем

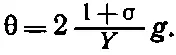
Или, если написать это в форме

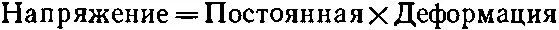
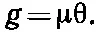(38.13)

Коэффициент пропорциональности μ называется модулем сдвига (или иногда коэффициентом жесткости). Вот как он выражается через Y и σ:

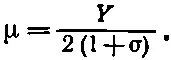(38.14)

Кстати, модуль сдвига должен быть положительным, иначе мы бы могли получить энергию от самопроизвольного сдвига кубика. Из уравнения (38.14) очевидно, что постоянная σ должна быть больше -1. Теперь мы знаем, что σ заключена между -1 и 1/ 2, но на практике, однако, она всегда больше нуля. В качестве последнего примера состояний подобного типа, когда напряженность постоянна по всему материалу, давайте рассмотрим задачу о бруске, который растягивается и в то же время закреплен таким образом, что боковое сокращение невозможно. (Технически немного легче сжимать брусок и сдерживать бока его от «распирания», но в сущности — это та же самая задача.) Что при этом происходит? На брусок должны действовать боковые силы, которые препятствуют изменению его толщины, — силы, которых мы не знаем непосредственно, но которые следует вычислить. Эта задача того же самого сорта, что мы решали, но только с немного другой алгеброй. Представьте себе силы, действующие на все три стороны, как это показано на фиг. 38.8.

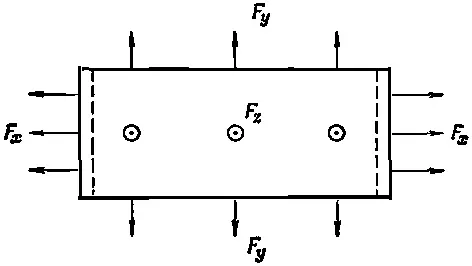
Фиг. 38.8. Растяжение без сокращения бокового размера.

Мы вычислим изменение размеров и подберем такие поперечные силы, чтобы ширина и высота оставались постоянными. Следуя обычным рассуждениям, мы получаем для трех напряжений

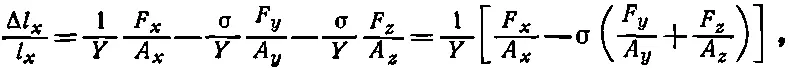(38.15)

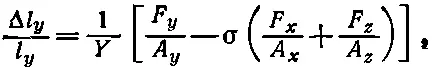(38.16)

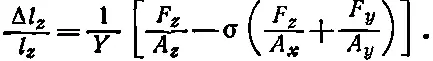(38.17)

Но поскольку по условию Δl уи Δl z равны нулю, то уравнения (38.16) и (38.17) дают два соотношения, связывающие F y и F z с F x . Совместно решая их, найдем

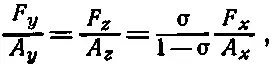(38.18)

а подставляя (38.18) в (38.15), получаем

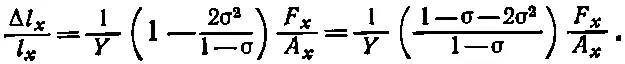(38.19)

Это соотношение вы часто можете встретить «перевернутым» и с преобразованным квадратичным полиномом по σ, т. е.

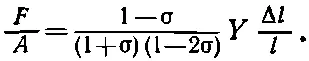(38.20)

Когда вы удерживаете бока, модуль Юнга умножается на некоторую сложную функцию σ. Из уравнения (38.19) можно сразу же увидеть, что множитель перед Y всегда больше единицы. Растянуть брусок, когда его бока удерживаются, гораздо труднее. Это означает также, что брусок становится жестче , когда его боковые стороны закреплены, нежели когда они свободны.

Обратимся теперь к более сложному примеру, когда различные части материала напряжены по-разному. Рассмотрим скрученный стержень — скажем, приводной вал какой-то машины или подвеску из кварцевой нити, применяемую в точных приборах. Из опытов с маятником кручения вы, по-видимому, знаете, что момент сил , действующий на закручиваемый стержень, пропорционален углу , причем константа пропорциональности, очевидно, зависит от длины стержня, его радиуса и свойств материала. Но каким образом — вот в чем вопрос? Теперь мы в состоянии ответить на него: просто нужно немного разобраться в геометрии.

На фиг. 38.9, а показан цилиндрический стержень, обладающий длиной L и радиусом а, один из концов которого закручен на угол φ по отношению к другому.

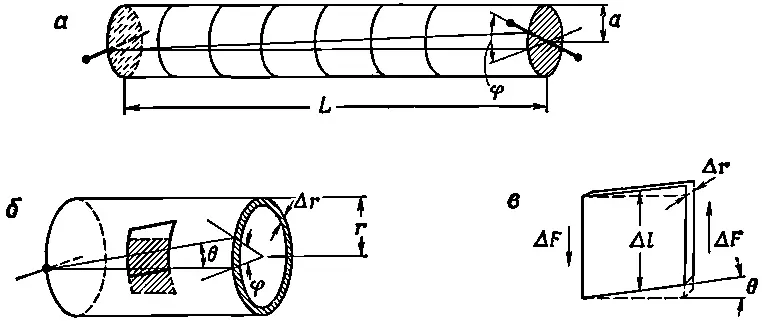
Фиг. 38.9. Кручение цилиндрического стержня (а), кручение цилиндрического слоя (б) и сдвиг любого маленького кусочка в слое (в).

Если мы хотим связать деформацию с тем, что уже известно, то стержень можно представить состоящим из множества цилиндрических оболочек и выяснить, что происходит в каждой из этих оболочек. Начнем с рассмотрения тонкого короткого цилиндра радиусом r (меньшего, чем в) и толщиной Δr, как показано на фиг. 38.9, б . Если теперь посмотреть на кусочек внутри этого цилиндра, который первоначально был маленьким квадратом, то можно заметить, что он превратился в параллелограмм. Каждый элемент цилиндра сдвигается, а угол сдвига θ равен

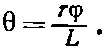
Поэтому напряжение сдвига g в материале будет [из уравнения (38.13)]

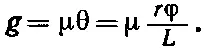(38.21)

Напряжение среза равно тангенциальной силе ΔF, действующей на конец квадратика, поделенной на его площадь ΔlΔr (см. фиг. 38.9, в ):

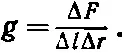
Сила ΔF, действующая на конец такого квадратика, создает относительно оси стержня момент сил Δτ, равный

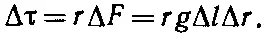(38.22)

Полный момент τ равен сумме таких моментов по всему периметру цилиндра. Складывая достаточное число таких кусков так, чтобы все Δl составляли 2πr, находим, что полный момент сил для пустотелой трубы равен