Ричард Фейнман - Том 2. Электромагнетизм и материя

Полное количество заряда, проходящее в единицу времени через какую-то поверхность S , называется электрическим током I . Он равен интегралу от нормальной составляющей потока по всем элементам поверхности (фиг. 13.3):

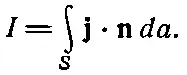(13.5)

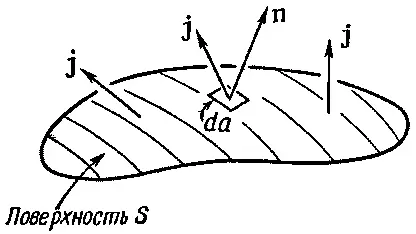
Фиг. 13.3. Ток I через поверхность S равен ∫j· nda

Ток I из замкнутой поверхности S представляет собой скорость, с которой заряды покидают объем V , окруженный поверхностью S . Один из основных законов физики говорит, что электрический заряд неуничтожаем ; он никогда не теряется и не создается. Электрические заряды могут перемещаться с места на место, но никогда не возникают из ничего. Мы говорим, что заряд сохраняется . Если из замкнутой поверхности возникает результирующий ток, то количество заряда внутри должно соответственно уменьшаться (фиг. 13.4).

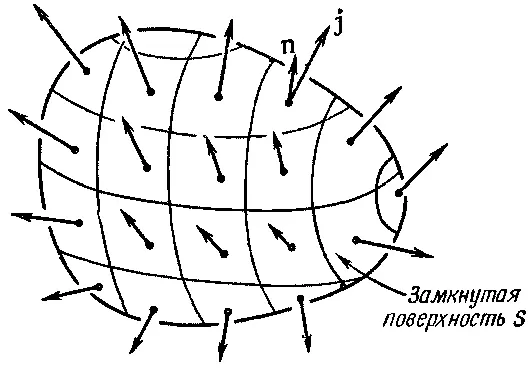
Фиг. 13.4. Интеграл от j·n по замкнутой поверхности равен скорости изменения полного заряда Q внутри.

Поэтому мы можем записать закон сохранения заряда в таком виде:

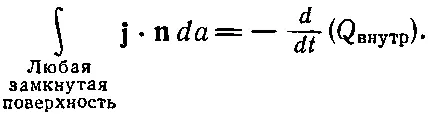(13.6)

Заряд внутри можно записать как объемный интеграл от плотности заряда

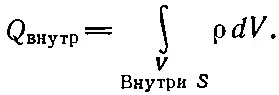(13.7)

Применяя (13.6) к малому объему ΔV, можно учесть, что интеграл слева есть ∇· jΔV. Заряд внутри равен ρΔV, поэтому сохранение заряда можно еще записать и так:

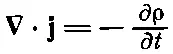(13.8)

(опять теорема Гаусса из математики!).

Теперь мы достаточно подготовлены, чтобы определить силу, действующую на находящуюся в магнитном поле проволоку, по которой идет ток. Ток состоит из заряженных частиц, движущихся по проволоке со скоростью v. Каждый заряд чувствует поперечную силу

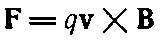
(фиг. 13.5, а).

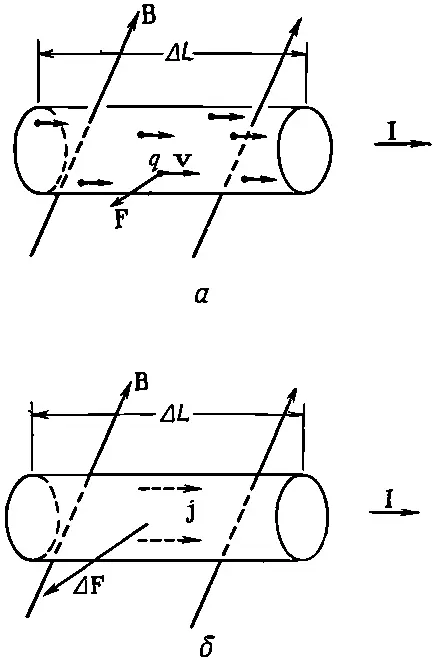
Фиг. 13.5. Магнитная сила на проволоку с током равна сумме сил на отдельные движущиеся заряды

Если в единичном объеме таких зарядов имеется N, то их число в малом объеме внутри проволоки ΔV равно N Δ V . Полная магнитная сила Δ F, действующая на объем ΔV, есть. сумма сил на отдельные заряды

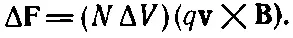
Но Nq vведь как раз равно j, так что

(13.9)

(фиг. 13.5, б ). Сила, действующая на единицу объема, равна j× B.

Если по проволоке с поперечным сечением А равномерно по сечению течет ток, то можно в качестве элемента объема взять цилиндр с основанием А и длиной ΔL. Тогда

(13.10)

Теперь можно jA назвать вектором тока Iв проволоке. (Его величина есть электрический ток в проволоке, а его направление совпадает с направлением проволоки.) Тогда

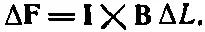(13.11)

Сила, действующая на единицу длины проволоки, есть I× B.

Это уравнение содержит важный результат — магнитная сила, действующая на проволоку и возникающая от движения в ней зарядов, зависит только от полного тока, а не от величины заряда, переносимого каждой частицей (и даже не зависит от его знака!). Магнитная сила, действующая на проволоку вблизи магнита, легко обнаруживается по отклонению проволоки при включении тока, как было нами описано в гл. 1 (см. фиг. 1.6).

Мы видели, что на проволоку в магнитном поле, создаваемом, скажем, магнитом, действует сила. Из закона о том, что действие равно противодействию, можно ожидать, что, когда по проволоке протекает ток [15] Потом мы увидим, что такие предположения, вообще говоря, неправильны для электромагнитных сил! , возникает сила, действующая на источник магнитного поля, т. е. на магнит. Такие силы действительно существуют; в этом можно убедиться по отклонению стрелки компаса вблизи проволоки с током. Далее, мы знаем, что магниты испытывают действие сил со стороны других магнитов, а отсюда вытекает, что когда по проволоке течет ток, то он создает собственное магнитное поле. Значит, движущиеся заряды создают магнитное поле. Попытаемся понять законы, которым подчиняются такие магнитные поля. Вопрос ставится так: дан ток, какое магнитное поле он создаст? Ответ на этот вопрос был получен экспериментально тремя опытами и подтвержден блестящим теоретическим доказательством Ампера. Мы не будем останавливаться на этой интересной истории, а просто скажем, что большое число экспериментов наглядно показало справедливость уравнений Максвелла. Их мы и возьмем в качестве отправной точки. Опуская в уравнениях члены с производными по времени, мы получаем уравнения магнитостатики

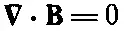(13.12)

и

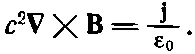(13.13)

Эти уравнения справедливы только при условии, что все плотности электрических зарядов и все токи постоянны, так что электрические и магнитные поля не меняются со временем — все поля «статические».

Можно тут заметить, что верить в существование статического магнитного поля довольно опасно, потому что вообще-то для получения магнитного поля нужны токи, а токи возникают только от движущихся зарядов. Следовательно, «магнитостатика» — только приближение.

Она связана с особым случаем динамики, когда движется большое число зарядов, которые можно приближенно описывать как постоянный поток зарядов. Только в этом случае можно говорить о плотности тока j, которая не меняется со временем. Более точно эту область следовало бы назвать изучением постоянных токов. Предполагая, что все поля постоянны, мы отбрасываем члены с ∂ E/∂ t и ∂ B/∂ t в полных уравнениях Максвелла [уравнения (2.41)] и получаем два написанных выше уравнения (13.12) и (13.13). Заметьте также, что поскольку дивергенция ротора любого вектора всегда нуль, то уравнение (13.13) требует, чтобы ∇· j=0. В силу уравнения (13.8) это верно, только если ∂ρ/∂ t =0. Но такое может быть, если Ене меняется со временем, следовательно, наши предположения внутренне согласованы.