Ричард Фейнман - Том 2. Электромагнетизм и материя

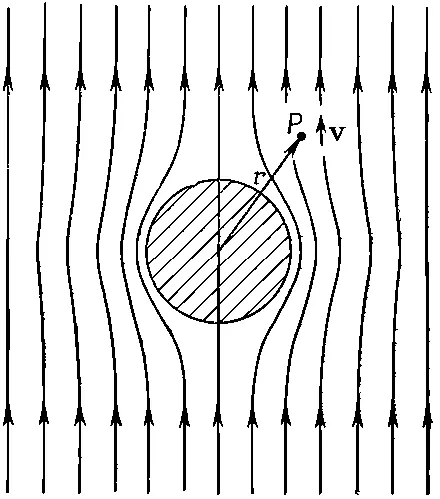
Фиг. 12.8. Поле скоростей безвихревого обтекания сферы жидкостью.

Эти линии, всегда параллельные v, соответствуют линиям напряженностей электрического поля. Мы хотим получить количественное описание поля скоростей, т. е. выражение для скорости в любой точке Р .

Можно найти скорость как градиент от ψ, поэтому сначала определим потенциал. Мы хотим найти потенциал, который удовлетворял бы всюду (12.31) при следующих двух условиях: 1) течение отсутствует в сферической области за поверхностью шара; 2) течение постоянно на больших расстояниях. Чтобы выполнялось первое ограничение, компонента v, перпендикулярная поверхности шара, должна обращаться в нуль. Это значит, что ∂ψ/∂ r =0 при r= а . Для выполнения второго ограничения нужно иметь ∂ψ/∂ z = v 0всюду, где r≫ а . Строго говоря, нет ни одной электростатической задачи, которая в точности соответствовала бы нашей задаче. Она фактически соответствует сфере с нулевой диэлектрической проницаемостью, помещенной в однородное электрическое поле. Если бы мы имели решение задачи для сферы с диэлектрической проницаемостью ϰ, то, положив ϰ=0, немедленно решили бы нашу задачу.

Мы раньше не разобрали такую электростатическую задачу во всех подробностях; давайте сделаем это сейчас. (Мы могли бы сразу решить задачу о жидкости с vи ψ, но будем пользоваться Еи φ, потому что привыкли к ним.)

Задача ставится так: найти такое решение уравнения ∇ 2φ=0, чтобы Е=- ∇φ равнялось постоянной, скажем Е 0, для больших r и, кроме того, чтобы радиальная компонента Ебыла равна нулю при r= а . Иначе говоря,

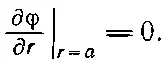(12.32)

Наша задача включает новый тип граничных условий — когда ∂φ/∂ r постоянно, а не тот, когда потенциал φ постоянен на поверхности. Это немножко другое условие. Получить ответ сразу нелегко. Прежде всего без шара φ был бы равен —E 0z. Тогда Ебыло бы направлено по z и имело бы всюду постоянную величину Е 0. Мы уже исследовали случай диэлектрического шара, поляризация внутри которого однородна, и нашли, что поле внутри поляризованного шара однородно, а вне его оно совпадает с полем точечного диполя, расположенного в центре шара. Давайте напишем, что искомое решение есть суперпозиция однородного поля плюс поле диполя. Потенциал диполя (см. гл. 6) есть pz/4πε 0r 3. Итак, мы предполагаем, что

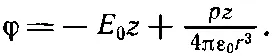(12.33)

Поскольку поле диполя спадает, как 1/r 3, то на больших расстояниях мы как раз имеем поле Е 0. Наше предположение автоматически удовлетворяет сформулированному выше второму условию (стр. 249). Но что нам взять в качестве силы диполя p? Для ответа мы должны использовать другое условие [уравнение (12.32)]. Мы должны продифференцировать φ по r, но, разумеется, это нужно сделать при постоянном угле θ, поэтому удобнее выразить сначала φ через r и θ, а не через z и r. Поскольку z=rcosθ, то

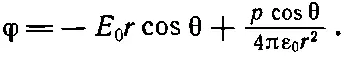(12.34)

Радиальная составляющая Е есть

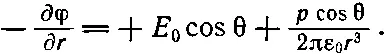(12.35)

Она должна быть равна нулю при r= а для всех θ. Это будет выполнено, если

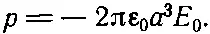(12.36)

Заметьте хорошенько, что если бы оба члена в уравнении (12.35) зависели бы от θ по-разному, то мы не смогли бы выбрать р так, чтобы (12.35) обращалось в нуль при r= а для всех углов. Тот факт, что это получилось, означает, что мы были мудры, написав уравнение (12.33). Конечно, когда мы догадывались, мы заглядывали вперед; мы знали, что понадобится еще один член, который бы, во-первых, удовлетворял ∇ 2φ=0 (любое действительное поле удовлетворяет этому), во-вторых, зависел от cosθ и, в-третьих, спадал бы к нулю при больших r. Поле диполя — единственное, которое удовлетворяет всем трем требованиям.

С помощью (12.36) наш потенциал приобретает вид

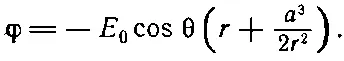(12.37)

Решение задачи о течении жидкости может быть записано просто:

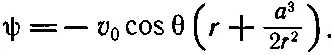(12.38)

Отсюда прямо находится v. Больше мы не будем заниматься этим вопросом.

В этом параграфе мы обратимся к совсем другой физической проблеме — мы ведь хотим показать большое разнообразие возможностей. На этот раз мы проделаем кое-что, что приведет нас к интегралу того же сорта, что мы нашли в электростатике. (Если перед нами стоит математическая задача, приводящая к некоторому интегралу, а интеграл этот уже знаком нам по другой задаче, то кое-что о его свойствах нам известно.) Возьмем пример из техники освещения. Пусть на расстоянии а над плоскостью имеется какой-то источник света. Как будет освещаться поверхность? Чему равна энергия излучения, падающая на единичную площадку поверхности за единицу времени (фиг. 12.9)?

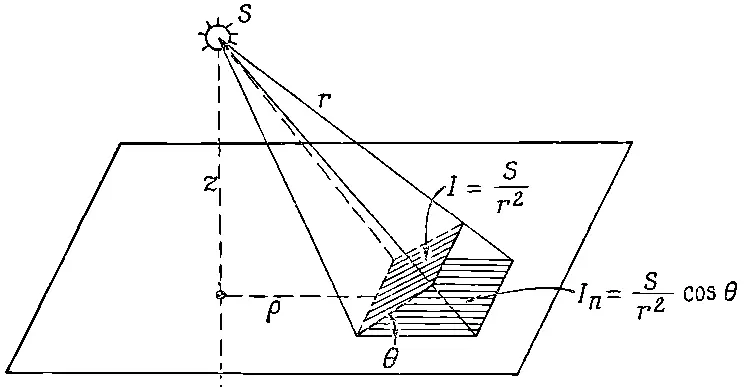
Фиг. 12.9. Освещенность I n поверхности равна энергии излучения, падающей в единицу времени на единичную площадку поверхности.

Мы предполагаем, что источник сферически-симметричный, так что свет излучается одинаково во всех направлениях. Тогда количество излученной энергии, проходящее через единичную площадку, перпендикулярную потоку света, меняется обратно пропорционально квадрату расстояния. Очевидно, что интенсивность света в направлении нормали дается такой же формулой, что и электрическое поле от точечного источника. Если световые лучи падают на поверхность под углом θ к нормали, то I , энергия, падающая на единичную площадку поверхности, уменьшается в cosθ раз, потому что та же энергия падает на площадь в 1/cosθ раз большую. Если мы назовем силу нашего источника S , тогда I n, освещенность поверхности, равна

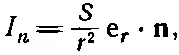(12.39)