Ричард Фейнман - Том 2. Электромагнетизм и материя

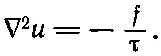(12.18)

Снова мы получили такое же уравнение, как в электростатике! Но на сей раз оно относится к двум измерениям. Смещение u соответствует φ, а f/τ соответствует ρ/ε 0. Поэтому тот труд, который мы потратили на бесконечные заряженные плоскости, или параллельные провода большой длины, или заряженные цилиндры, пригодится для натянутой мембраны.

Предположим, мы подтягиваем мембрану в каких-то точках на определенную высоту , т. е. фиксируем величину и в ряде точек. В электрическом случае это аналогично заданию определенного потенциала в соответствующих местах. Например, мы можем устроить положительный «потенциал», если подопрем мембрану предметом, который имеет такое же сечение, как и соответствующий цилиндрический проводник. Если, скажем, мы подопрем мембрану круглым стержнем, поверхность примет форму, изображенную на фиг. 12.6.

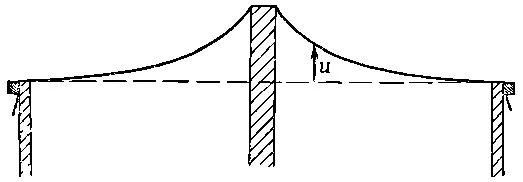
Фиг. 12.6. Поперечное сечение натянутой резиновой пленки, подпертой круглым стержнем. Функция u(х, у) та же, что и потенциал φ(х, у) от очень длинного заряженного стержня.

Высота и имеет такой же вид, как электростатический потенциал φ заряженного цилиндрического стержня. Она спадает, как ln(1/r). ( Наклон поверхности, который соответствует электрическому полю Е, спадает, как 1/r.)

Натянутую резиновую пленку часто использовали для решения сложных электрических задач экспериментальным путем. Аналогия используется в обратную сторону! Для подъема мембраны на высоту, соответствующую потенциалам всего набора электродов, подставляют разные стержни и полоски. Затем измерения высоты дают электрический потенциал в электростатической задаче. Аналогия проводится даже еще дальше. Если на мембране поместить маленькие шарики, то их движение примерно схоже с движением электронов в соответствующем электрическом поле. Таким способом можно воочию проследить за движением «электронов» по их траекториям. Этот метод был использован для проектирования сложной системы многих фотоумножительных трубок (таких, например, какие используются в сцинтилляционном счетчике или для управления передними фарами в автомашине кадиллак). Метод используется и до сих пор, но его точность не очень велика. Для более точных расчетов лучше находить поле численным путем с помощью больших электронных вычислительных машин.

Приведем еще один пример, дающий уравнение того же вида, но на сей раз относящееся к диффузии. В гл. 43 (вып. 4) мы рассмотрели диффузию ионов в однородном газе и диффузию одного газа сквозь другой. Теперь возьмем другой пример — диффузию нейтронов в материале типа графита. Мы выбрали графит (разновидность чистого углерода), потому что углерод не поглощает медленных нейтронов. Нейтроны путешествуют в нем свободно. Они проходят по прямой в среднем несколько сантиметров, прежде чем рассеются ядром и отклонятся в сторону. Так что если у нас есть большой кусок графита толщиной в несколько метров, то нейтроны, находившиеся сначала в одном месте, будут переходить в другие места. Мы опишем их усредненное поведение, т. е. их средний поток .

Пусть N ( x, у, z )ΔV — число нейтронов в элементе объема ΔV в точке ( х, у, z ). Движение нейтронов приводит к тому, что одни покидают ΔV, а другие попадают в него. Если в одной области оказывается нейтронов больше, чем в соседней, то оттуда их будет переходить во вторую область больше, чем наоборот; в результате возникнет поток. Повторяя доказательства, приведенные в гл. 43 (вып. 4), можно описать поток вектором потока J. Его компонента J x есть результирующее число нейтронов, проходящих в единицу времени через единичную площадку, перпендикулярную оси х . Мы получим тогда

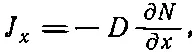(12.19)

где коэффициент диффузии D дается в терминах средней скорости v и средней длины свободного пробега l между столкновениями:

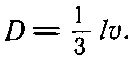
Векторное уравнение для Jимеет вид

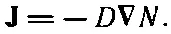(12.20)

Скорость, с которой нейтроны проходят через некоторый элемент поверхности da , равна J· n da (где n, как обычно,— единичный вектор нормали). Результирующий поток из элемента объема тогда равен (пользуясь обычным гауссовым доказательством) ∇· J dV . Этот поток приводил бы к уменьшению числа нейтронов в ΔV, если нейтроны не генерируются внутри ΔV (с помощью какой-нибудь ядерной реакции). Если в объеме присутствуют источники, производящие S нейтронов в единицу времени в единице объема, то результирующий поток из ΔV будет равен [ S -(∂ N /∂ t )]ΔV. Тогда получаем

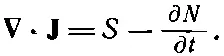(12.21)

Комбинируя (12.21) и (12.20), получаем уравнение диффузии нейтронов

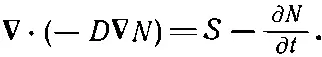(12.22)

В статическом случае, когда ∂ N /∂ t =0, мы снова имеем уравнение (12.4)! Мы можем воспользоваться нашими знаниями в электростатике для решения задач по диффузии нейтронов. Давайте же решим какую-нибудь задачу. (Пожалуй, вы недоумеваете: зачем решать новую задачу, если мы уже решили все задачи в электростатике? На этот раз мы можем решить быстрее именно потому, что электростатические задачи действительно уже решены !)

Пусть имеется блок материала, в котором нейтроны (скажем, за счет деления урана) рождаются равномерно в сферической области радиусом а (фиг. 12.7).

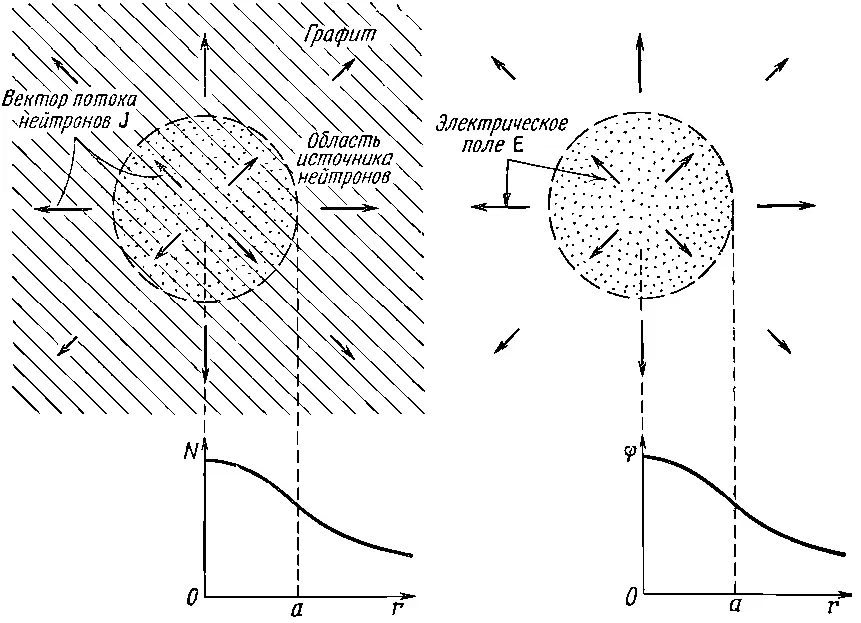
Фиг. 12.7. Нейтроны рождаются однородно внутри сферы радиуса а в большом графитовом блоке и диффундируют наружу. Плотность нейтронов N получена как функция r, расстояния от центра источника. Справа показана электростатическая аналогия: однородно заряженная сфера, причем N соответствует φ, а J соответствует Е.

Мы хотели бы узнать, чему равна плотность нейтронов повсюду? Насколько однородна плотность нейтронов в области, где они рождаются? Чему равно отношение нейтронной плотности в центре к нейтронной плотности на поверхности области рождения? Ответы найти легко. Плотность нейтронов в источнике S 0стоит вместо плотности зарядов ρ, поэтому наша задача такая же, как задача об однородно заряженной сфере. Найти N —все равно, что найти потенциал φ. Мы уже нашли поля внутри и вне однородно заряженной сферы; для получения потенциала мы можем их проинтегрировать. Вне сферы потенциал равен Q/4πε 0r, где полный заряд Q дается отношением 4πа 3ρ/3. Следовательно,