Ричард Фейнман - Том 2. Электромагнетизм и материя

В задаче об электрическом поле мы придумали решение, вообразив за проводящей плоскостью точечный заряд. Можно воспользоваться снова этой же идеей. Попытаемся выбрать такое «изображение» источника, которое автоматически обращало бы в нуль нормальную компоненту поля вблизи поверхности. Решение показано на фиг. 12.2. Электрическое изображение источника с тем же знаком и той же величины, находящееся на расстоянии а над поверхностью, дает поле, горизонтальное повсюду у поверхности. Нормальные компоненты от обоих источников взаимно уничтожаются.

Итак, наша задача о потоке тепла решена. Температура во всем пространстве одинакова по непосредственной аналогии с потенциалом от двух одинаковых точечных зарядов. Температура Т на расстоянии r от одного точечного источника G в бесконечной среде равна

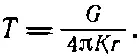(12.13)

(Это, конечно, полностью аналогично φ=q/4πε 0r.) Температура точечного источника и, кроме того, его изображения равна

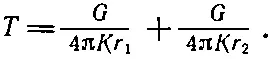(12.14)

Эта формула дает нам температуру всюду внутри блока. Несколько изотермических поверхностей приведено на фиг. 12.2.

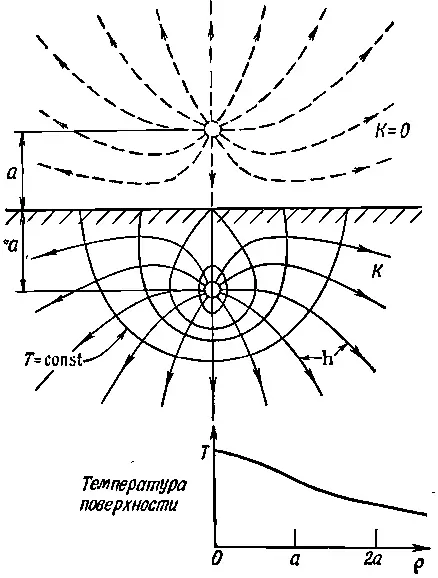
Фиг. 12.2. Поток тепла и изотерма у точечного источника тепла, расположенного на расстоянии а под поверхностью тела с хорошей теплопроводностью. Вне тела показано мнимое изображение источника.

Показаны также линии h, которые можно получить из выражения h=-К∇Т.

В самом начале мы интересовались распределением температуры на поверхности. Для точки на поверхности находящейся на расстоянии ρ от оси, r 1=r 2=√(ρ 2+а 2), следовательно,

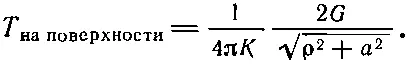(12.15)

Эта функция также изображена на фиг. 12.2. Естественно, что температура прямо над источником выше, чем вдали от него. Такого рода задачи часто приходится решать геофизикам. Теперь мы видим, что это те же самые задачи, которые мы решали в электричестве.

Рассмотрим теперь совсем другую область физики, в которой тем не менее мы придем снова к точно таким же уравнениям. Возьмем тонкую резиновую пленку — мембрану, натянутую на большую горизонтальную раму (наподобие кожи на барабане). Нажмем на мембрану в одном месте вверх, а в другом — вниз (фиг. 12.3). Сможем ли мы описать форму поверхности? Покажем, как можно решить эту задачу, когда отклонения мембраны не очень велики.

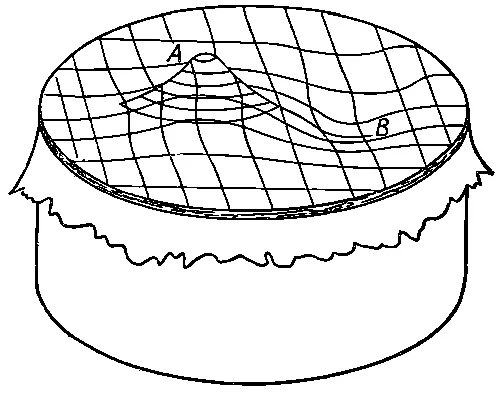
Фиг. 12.3. Тонкая резиновая пленка, натянутая на цилиндр (нечто вроде барабана). Какой формы будет поверхность, если пленку приподнять в точке A и опустить в точке В?

В пленке действуют силы, потому что она натянута. Если сделать в каком-нибудь месте пленки небольшой разрез, то два края разреза разойдутся (фиг. 12.4). Следовательно, в пленке имеется поверхностное натяжение , аналогичное одномерному натяжению растянутой веревки. Определим величину поверхностного натяжения τ как силу на единицу длины , которая как раз удержала бы вместе две стороны разреза (см. фиг. 12.4).

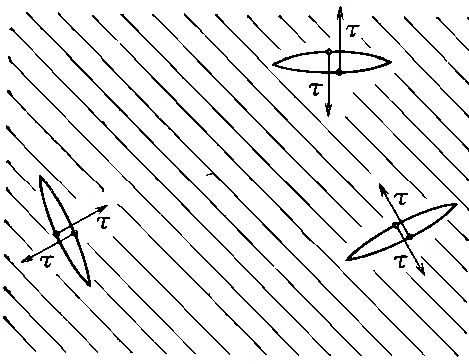
Фиг. 12.4. Поверхностное натяжение τ натянутой, резиновой пленки есть сила отнесенная к единице длины и направленная перпендикулярно линии разреза.

Предположим теперь, что мы смотрим на вертикальное поперечное сечение мембраны. Оно будет иметь вид некоторой кривой, похожей на изображенную на фиг. 12.5. Пусть и — вертикальное смещение мембраны от ее нормального положения, а х и у — координаты в горизонтальной плоскости. (Приведенное сечение параллельно оси х .)

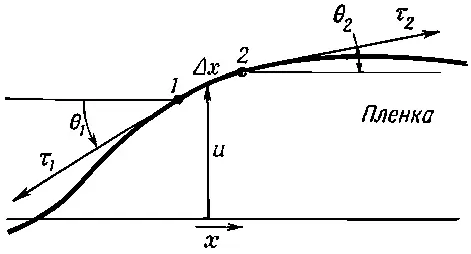
Фиг. 12.5. Поперечное сечение изогнутой пленки.

Возьмем небольшой кусочек поверхности длиной Δx и шириной Δу. На него действуют силы вследствие поверхностного натяжения вдоль каждого края. Сила на стороне 1 (см. фиг. 12.5) будет равна τ 1Δy и направлена по касательной к поверхности, т. е. под углом θ 1к горизонтали. Вдоль стороны 2 сила будет равна τ 2Δy и направлена к поверхности под углом θ 2. (Подобные силы будут и на двух других сторонах кусочка, но мы пока забудем о них.) Результирующая сила от сторон 1 и 2, действующая на кусочек вверх , равна

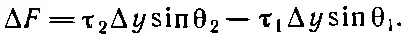
Мы ограничимся рассмотрением малых искажений мембраны, т. е. малых изгибов и наклонов : тогда мы сможем заменить sinθ на tgθ и записать как ∂ u /∂ x . Сила при этих условиях дается выражением

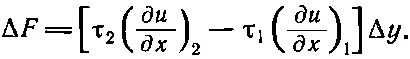
Величина в скобках может быть с тем же успехом записана (для малых Δx) как

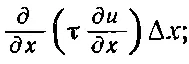
тогда

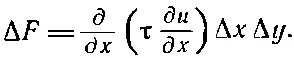
Имеется и другой вклад в Δ F от сил на двух других сторонах; полный вклад, очевидно, равен

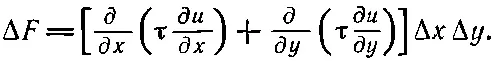(12.16)

Искривления диафрагмы вызваны внешними силами. Пусть f означает направленную вверх силу на единичную площадку пленки (своего рода «давление»), возникающую от внешних сил . Если мембрана находится в равновесии ( статический случай), то сила эта должна уравновешиваться только что вычисленной внутренней силой [уравнение (12.16)]. Иначе говоря,

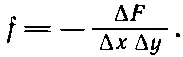
Уравнение (12.16) тогда может быть записано в виде

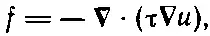(12.17)

где под знаком ∇ мы теперь подразумеваем, конечно, двухмерный оператор градиента (∂/∂ x , ∂/∂ y ). У нас есть дифференциальное уравнение, связывающее u ( х, у ) с приложенными силами f ( x, у ) и поверхностным натяжением пленки τ( x, у ), которое, вообще говоря, может меняться от места к месту. (Деформации трехмерного упругого тела тоже подчиняются таким уравнениям, но мы ограничимся двухмерным случаем.) Нас будет интересовать только случай, когда натяжение τ постоянно по всей пленке. Тогда вместо (12.17) мы можем записать