Ричард Фейнман - Том 2. Электромагнетизм и материя

Вернемся к нашему атомному описанию проволоки, по которой идет ток. В обычном проводнике, вроде меди, электрические токи возникают за счет движения части отрицательных электронов (называемых электронами проводимости), тогда как положительные ядерные заряды и остальные электроны остаются закрепленными внутри материала. Пусть плотность электронов проводимости есть ρ, а их скорость в системе S есть v. Плотность неподвижных зарядов в системе S есть ρ +, что должно быть равно ρ -с обратным знаком, потому что мы берем незаряженную проволоку. Поэтому вне проволоки электрического поля нет, и сила на движущуюся частицу равна просто

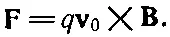
Используя результат, найденный нами в уравнении (13.18) для магнитного поля на расстоянии r от оси проволоки, мы заключаем, что сила, действующая на частицу, направлена к проволоке и равна по величине

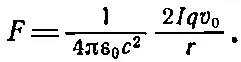
С помощью уравнений (13.4) и (13.5) ток I может быть записан как ρ +vA, где А — площадь поперечного сечения проволоки. Тогда

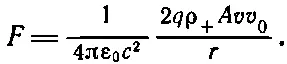(13.20)

Мы могли бы продолжить рассмотрение общего случая произвольных скоростей v и v 0, но ничуть не хуже будет взять частный случай, когда скорость v 0частицы совпадает со скоростью v электронов проводимости. Поэтому мы запишем v = v 0, и уравнение (13.20) приобретет вид

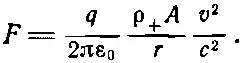(13.21)

Теперь обратимся к тому, что происходит в системе S ', где частица покоится и проволока бежит мимо нее (влево на фиг. 13.10, б) со скоростью v . Положительные заряды, движущиеся вместе с проволокой, создадут около частицы некоторое магнитное поле В '. Но частица теперь покоится , так что магнитная сила на нее не действует! Если и возникает какая-то сила, то она должна появиться за счет электрического поля. Выходит, что движущаяся проволока создает электрическое поле. Но она может это сделать, только если она кажется заряженной ; должно получаться так, чтобы нейтральная проволока с током казалась заряженной, если ее привести в движение.

Нужно в этом разобраться. Попробуем вычислить плотность зарядов в проволоке в системе S', пользуясь тем, что мы знаем о ней в системе S . На первый взгляд можно было бы подумать, что плотности одинаковы, но из гл. 15 (вып. 2) мы знаем, что при переходе от одной системы к другой длины меняются, следовательно, объемы также изменятся. Поскольку плотности зарядов зависят от объема, занимаемого зарядами, плотности будут также меняться.

Прежде чем определить плотности зарядов в системе S ', нужно знать, что происходит с электрическим зарядом группы электронов, когда заряды движутся. Мы знаем, что кажущаяся масса частицы приобретает множитель 1/√(1-v 2/c 2). Происходит ли что-нибудь подобное с ее зарядом? Нет! Заряды никогда не меняются независимо от того, движутся ли они или нет. Иначе мы не могли бы наблюдать на опыте сохранение полного заряда.

Возьмем кусок вещества, например проводника, и пусть он вначале незаряжен. Теперь нагреем его. Поскольку масса электронов иная, чем у протонов, скорости электронов и протонов изменятся по-разному. Если бы заряд частицы зависел от скорости частицы, которая его переносит, то в нагретом куске заряды электронов и протонов не были бы скомпенсированы. Кусок материала при нагревании становился бы заряженным.

Мы видели раньше, что очень малое изменение заряда у каждого из электронов в куске привело бы к огромным электрическим полям. Ничего подобного никогда не наблюдалось.

Кроме того, можно заметить, что средняя скорость электронов в веществе зависит от его химического состава. Если бы заряд электрона менялся со скоростью, суммарный заряд в куске вещества изменялся бы в ходе химической реакции. Как и раньше, прямое вычисление показывает, что даже совсем малая зависимость заряда от скорости привела бы в простейших химических реакциях к огромным полям. Ничего похожего не наблюдалось, и мы приходим к выводу, что электрический заряд отдельной частицы не зависит от состояния движения или покоя.

Итак, заряд частицы q есть инвариантная скалярная величина, не зависящая от системы отсчета. Это означает, что в любой системе плотность зарядов у некоторого распределения электронов просто пропорциональна числу электронов в единице объема. Нам нужно только учесть тот факт, что объем может меняться из-за релятивистского сокращения расстояний.

Применим теперь эти идеи к нашей движущейся проволоке. Если взять проволоку длиной L 0, в которой плотность неподвижных зарядов есть ρ 0, то в ней будет содержаться полный заряд Q =ρ 0 L 0 A 0. Если те же заряды движутся в другой системе со скоростью v , то они все будут находиться в куске материала меньшей длины

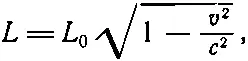(13.22)

но того же сечения A 0, поскольку размеры в направлении, перпендикулярном движению, не меняются (фиг. 13.11).

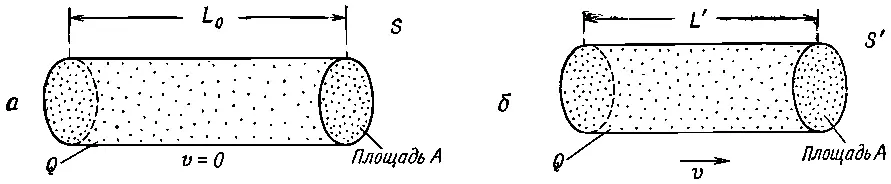
Фиг. 13.11 .Если распределение заряженных частиц имеет плотность зарядов р 0 , то с точки зрения системы, движущейся с относительной скоростью v, плотность зарядов будет равна ρ=ρ 0 /√(1 — v 2 /с 2 ).

Если через ρ обозначить плотность зарядов в системе, где они движутся, то полный заряд Q будет ρ LA 0. Но это должно быть также равно ρ 0 L 0 А , потому что заряд в любой системе одинаков, следовательно, ρL=ρ 0L 0, или с помощью (13.22)

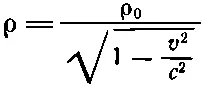(13.23)

Плотность зарядов движущейся совокупности зарядов меняется таким же образом, как и релятивистская масса частицы.

Применим теперь этот результат к плотности положительных зарядов ρ +в нашей проволоке. Эти заряды покоятся в системе S . Однако в системе S', где проволока движется со скоростью v , плотность положительных зарядов становится равной

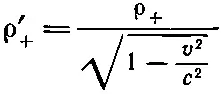(13.24)

Отрицательные заряды в системе S ' покоятся, поэтому их плотность в этой системе есть «плотность покоя» ρ 0. В уравнении (13.23) ρ' 0=ρ' -, потому что их плотность зарядов равна ρ -,если проволока покоится, т. е. в системе S, где скорость отрицательных зарядов равна v . Тогда для электронов проводимости мы получаем