Ричард Фейнман - Том 2. Электромагнетизм и материя

В электростатике, как мы видели (из-за того, что rot от Евезде равен нулю), всегда можно представить Ев виде градиента от скалярного поля φ. А вот rot от В не везде равен нулю, поэтому представить его в виде градиента, вообще говоря, невозможно. Однако дивергенция Ввезде равна нулю, а это значит, что мы можем представить Вв виде ротора от другого векторного поля. Ибо, как мы видели в гл. 2, § 8, дивергенция ротора всегда равна нулю. Следовательно, мы всегда можем выразить В через поле, которое мы обозначим А:

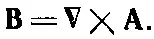(14.3)

Или, расписывая компоненты:

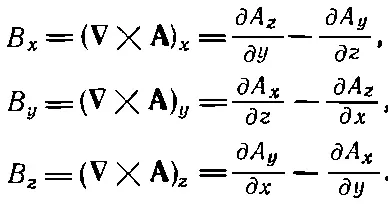(14.4)

Запись B=∇×A гарантирует выполнение (14.1), потому что обязательно

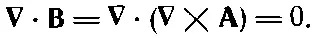
Поле Аназывается векторным потенциалом .

Вспомним, что скалярный потенциал φ оказывается не полностью определенным. Если мы нашли для некоторой задачи потенциал φ, то всегда можно найти столь же хороший другой потенциал φ', добавив постоянную:

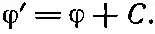
Новый потенциал φ' дает те же электрические поля, потому что градиент ∇ Сесть нуль; φ' и φ отвечают одной и той же картине.

Точно так же у нас может быть несколько векторных потенциалов А, приводящих к одним и тем же магнитным полям. Опять-таки, поскольку Вполучается из Адифференцированием, то прибавление к Аконстанты не меняет физики дела. Но для Асвобода больше. Мы можем добавить к Алюбое поле, которое есть градиент от некоторого скалярного поля, не меняя при этом физики. Это можно показать следующим образом. Пусть у нас есть А, которое в какой-то реальной задаче дает правильное поле В. Спрашивается, при каких условиях другой векторный потенциал А', будучи подставлен в (14.3), дает то же самое поле В. Значит, Аи А' имеют одинаковый ротор

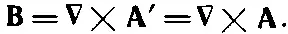
Поэтому

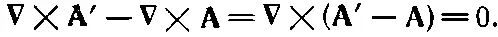
Но если ротор вектора есть нуль, то вектор должен быть градиентом некоторого скалярного поля, скажем ψ, так что А'- A=∇ψ. Это означает, что если Аесть векторный потенциал, отвечающий данной задаче, то при любом ψ

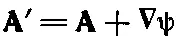(14.5)

также будет векторным потенциалом, в одинаковой степени удовлетворяющим данной задаче и приводящим к тому же полю В.

Обычно бывает удобно уменьшить «свободу» А, накладывая на него произвольно некоторое другое условие (почти таким же образом мы считали удобным — довольно часто — выбирать потенциал φ равным нулю на больших расстояниях). Мы можем, например, ограничить А, наложив на него такое условие, чтобы дивергенция Ачему-нибудь равнялась. Мы всегда можем это сделать, не задевая В. Так получается потому, что, хотя А' и Аимеют одинаковый ротор и дают одно и то же В, они вовсе не обязаны иметь одинаковую дивергенцию. В самом деле, ∇· A'=∇· A+∇ 2ψ, и, подбирая соответствующее ψ, можно придать ∇· A' любое значение.

Чему следует приравнять ∇· А? Выбор должен обеспечить наибольшее математическое удобство и зависит от нашей задачи. Для магнитостатики мы сделаем простой выбор

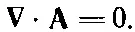(14.6)

(Потом, когда мы перейдем к электродинамике, мы изменим наш выбор.) Итак, наше полное определение [17] Наше определение все еще не полностью задает А . Чтобы задание было единственным, мы должны были бы что-нибудь сказать о поведении поля А на какой-либо границе или на больших расстояниях. Иногда бывает удобно выбрать, например, поле, спадающее к нулю на больших расстояниях. А в данный момент есть ∇× A= Bи ∇· А=0.

Чтобы привыкнуть к векторному потенциалу, посмотрим сначала, чему он равен для однородного магнитного поля В 0. Выбирая ось z в направлении В 0, мы должны иметь

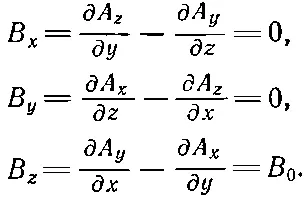(14.7)

Рассматривая эти уравнения, мы видим, что одно из возможных решений есть

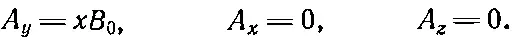
Или с тем же успехом можно взять

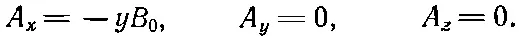
Еще одно решение есть комбинация первых двух

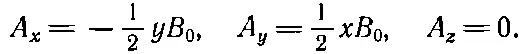(14.8)

Ясно, что для каждого поля Ввекторный потенциал Ане единственный; существует много возможностей.

Третье решение [уравнение (14.8)] обладает рядом интересных свойств. Поскольку x-компонента пропорциональна -y, а y-компонента пропорциональна + x , то вектор Aдолжен быть перпендикулярен вектору, проведенному от оси z, который мы обозначим r' (штрих означает, что это не вектор расстояния от начала). Кроме того, величина Апропорциональна √(x 2+y 2) и, следовательно, пропорциональна r '. Поэтому А(для однородного поля) может быть записано просто

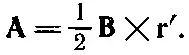(14.9)

Векторный потенциал Аравен по величине Br '/2, и вращается вокруг оси z , как показано на фиг. 14.1.

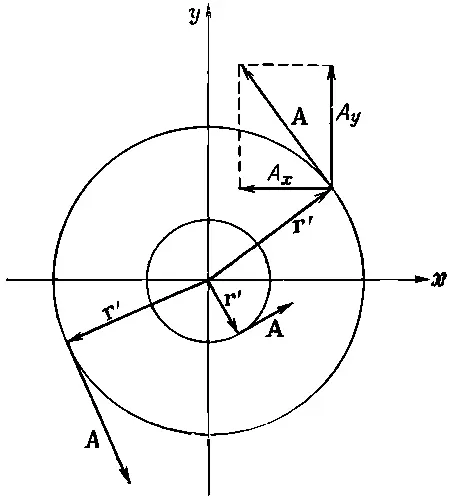
Фиг. 14.1. Однородное магнитное поле В, направленное по оси z, соответствует векторному потенциалу А (А=Вr'/2), который вращается вокруг оси z. т' — расстояние до оси z.

Если, например, поле Весть поле внутри соленоида вдоль его оси, то векторный потенциал циркулирует точно таким же образом, как и токи в соленоиде.