Ричард Фейнман - Том 2. Электромагнетизм и материя

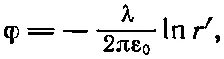
где r'=√(x 2+y 2), а λ — заряд на единицу длины πа 2ρ. Следовательно, А z должно быть равно

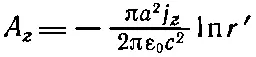
для точек вне длинного провода с равномерно распределенным током. Поскольку πа 2j z=I, то можно также написать

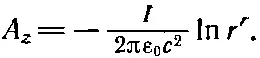(14.21)

Теперь можно найти В, пользуясь (14.4). Из шести производных от нуля отличны только две. Получаем

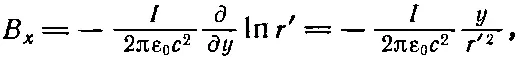(14.22)

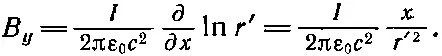(14.23)

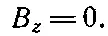
Мы получаем тот же результат, что и раньше: Вобходит провод по окружности и по величине равен

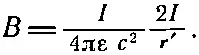(14.24).

Еще пример. Рассмотрим опять бесконечно длинный соленоид с током по окружности, равным nI на единицу длины. (Мы считаем, что имеется n витков проволоки на единицу длины, несущих каждый ток I, и пренебрегаем небольшими зазорами между витками.)

Точно так же, как мы выводили «поверхностную плотность заряда» σ, определим здесь «поверхностную плотность тока» J, равную току на единице длины по поверхности соленоида (что, конечно, есть просто среднее j, умноженное на толщину тонкой намотки). Величина Jздесь равна nI .

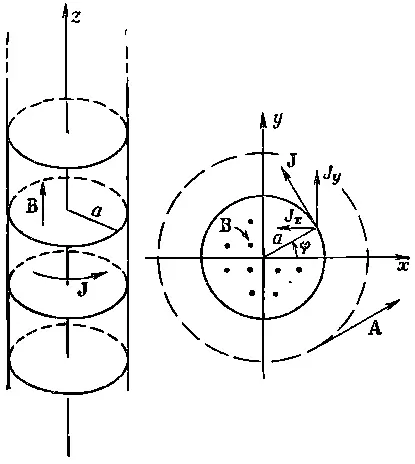
Фиг. 14.4. Длинный соленоид с поверхностной плотностью тока J.

Этот поверхностный ток (фиг. 14.4) имеет компоненты

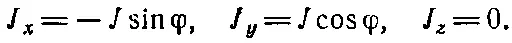
Мы должны теперь найти Адля такого распределения токов.

Прежде всего найдем А х в точках вне соленоида. Результат такой же, как электростатический потенциал вне цилиндра с поверхностным зарядом:

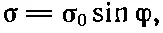
где σ 0=- J / c 2. Мы не решали случай такого распределения заряда, но делали нечто похожее. Это распределение заряда эквивалентно двум жестким цилиндрам, состоящим из зарядов, один из положительных, другой из отрицательных, с малым относительным смещением их осей в направлении у . Потенциал такой пары цилиндров пропорционален производной по у от потенциала одного однородно заряженного цилиндра. Мы, конечно, можем вычислить константу пропорциональности, но пока не будем возиться с этим.

Потенциал заряженного цилиндра пропорционален ln r '; потенциал пары тогда равен

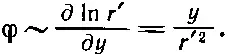
Итак, мы знаем, что

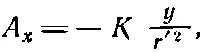(14.25)

где К — некоторая константа. Рассуждая точно так же, найдем

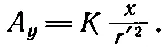(14.26)

Хотя мы раньше говорили, что вне соленоида магнитного поля нет, теперь мы находим, что поле Асуществует и циркулирует вокруг оси z (см. фиг. 14.4). Возникает вопрос: равен ли нулю его ротор?

Очевидно, В х и В y равны нулю, а

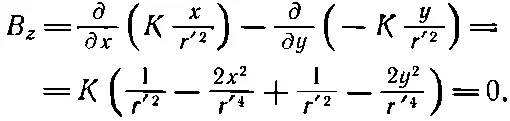
Итак, магнитное поле вне очень длинного соленоида действительно равно нулю, хотя векторный потенциал нулю не равен.

Мы можем проверить наш результат, прибегнув к другим соображениям. Циркуляция векторного потенциала вокруг соленоида должна равняться потоку В внутри катушки [уравнение (14.11)]. Циркуляция равна А ·2π r ' или, поскольку А = К / r ', она равна 2π К . Заметьте, что циркуляция не зависит от r'. Так и должно быть, если Ввне соленоида отсутствует, потому что поток есть просто величина В внутри соленоида, умноженная на πа 2. Он один и тот же для всех окружностей с радиусом r'>а. Раньше мы нашли, что поле внутри равно nI /ε 0c 2, поэтому мы можем определить константу К :

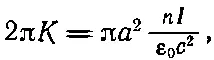
или

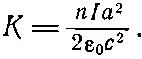
Итак, векторный потенциал снаружи имеет величину

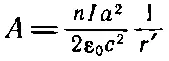(14.27)

и всегда перпендикулярен вектору r'.

Мы говорили о соленоидальной катушке из проволоки, но такое же поле мы могли бы создать, вращая длинный цилиндр с электростатическим зарядом на поверхности. Если у нас есть тонкий цилиндрический слой радиуса а с поверхностным зарядом σ, то вращение цилиндра образует поверхностный ток J =σ v , где v= a ω — скорость поверхностного заряда. Внутри цилиндра тогда будет магнитное поле B =σ a ω/ε 0с 2.

Теперь можно поставить интересный вопрос. Предположим, что перпендикулярно к оси цилиндра мы поместили короткий отрезок проволоки W от оси до поверхности и прикрепили ее к цилиндру так, что проволока вращается вместе с ним (фиг. 14.5).

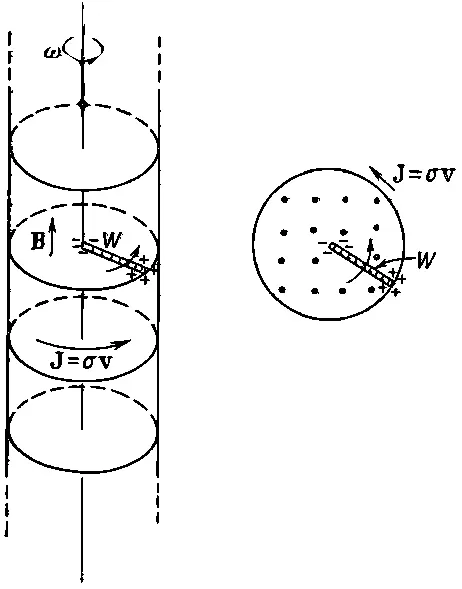
Фиг. 14.5. Вращающийся заряженный цилиндр создает внутри себя магнитное поле. Короткая проволока, закрепленная вдоль радиуса, вращаясь вместе с цилиндром, приобретает на своих концах индуцированные заряды.

Эта проволока движется в магнитном поле, так что сила v× Bприведет к тому, что концы проволоки зарядятся (они будут заряжаться до тех пор, пока поле Езарядов не уравновесит силы v× B). Если цилиндр заряжен положительно, то конец проволоки вблизи оси будет иметь отрицательный заряд. Измеряя заряд на конце проволоки, мы могли бы определить скорость вращения системы. Мы получили бы «угловой скоростемер» (или «угловой ситометр»)!