Ричард Фейнман - Том 2. Электромагнетизм и материя

Но вы, наверно, засомневаетесь: «А что, если я сам перейду,— скажете вы,— в систему координат вращающегося цилиндра? Там заряженный цилиндр покоится, а я знаю из электростатических уравнений, что внутри цилиндра никакого поля не будет , не будет и силы, толкающей заряды к центру. Поэтому здесь что-то не так?» Нет. Все правильно. «Относительности вращения» не существует. Вращающаяся система — не инерциальная система, и законы физики в ней другие. Мы должны пользоваться уравнениями электромагнетизма только в инерциальных системах координат.

Было бы здорово, если бы смогли измерить абсолютное вращение Земли с помощью такого заряженного цилиндра, но эффект, к несчастью, настолько мал, что его невозможно наблюдать даже с помощью самых тонких современных приборов.

Воспользуемся методом векторного потенциала, чтобы найти магнитное поле маленькой петли с током. Как обычно, под словом «маленькая» мы просто подразумеваем, что нас интересуют поля только на больших расстояниях по сравнению с размером петли. Как мы увидим, любая петелька представляет собой «магнитный диполь». Это значит, что она создает магнитное поле, подобное электрическому полю от электрического диполя.

Возьмем сначала прямоугольную петлю и выберем оси координат, как показано на фиг. 14.6.

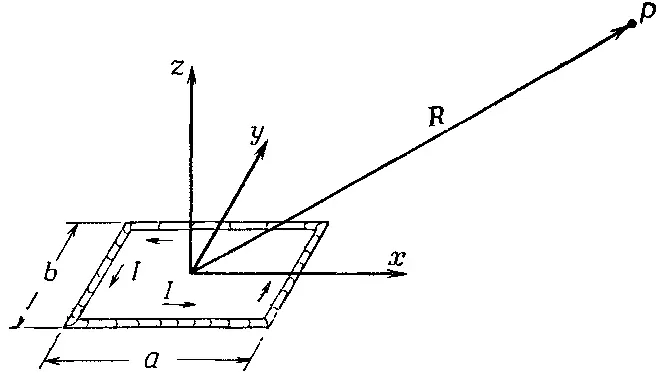
Фиг. 14.6. Прямоугольная проволочная петля с током I. Чему равно магнитное поле в точке P? (R≫a и b).

Токов в направлении z нет, поэтому A z равно нулю. Есть токи в направлении х по обеим сторонам прямоугольника, длина которых а . В каждой стороне плотность тока и ток однородны. Поэтому решение для А х в точности подобно электростатическому потенциалу от двух заряженных палочек (фиг. 14.7).

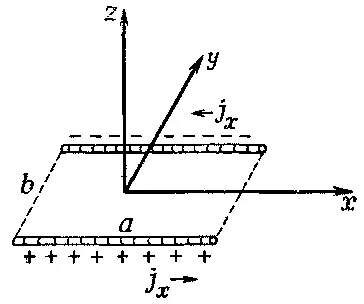
Фиг. 14.7. Распределение j x в проволочной петле о током, изображенной на фиг. 14.6.

Поскольку палочки имеют противоположные заряды, их электрический потенциал на больших расстояниях есть как раз дипольный потенциал (см. гл. 6, § 5). В точке Р на фиг. 14.6 потенциал равен

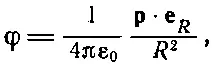(14.28)

где р— дипольный момент распределения зарядов. В данном случае дипольный момент равен полному заряду на одной палочке, умноженному на расстояние между ними:

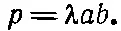(14.29)

Дипольный момент смотрит в отрицательном направлении y, поэтому косинус угла между Rи рравен — y / R (где у — координата Р ). Итак, мы имеем

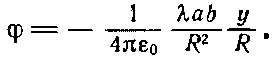
Заменяя λ на I/с 2, сразу же получаем А х :

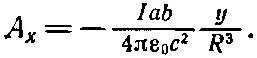(14.30)

С помощью тех же рассуждений:

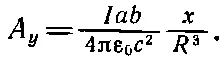(14.31)

Снова А у пропорционально х , а А х пропорционально —y, так что векторный потенциал (на больших расстояниях) идет по кругу вокруг оси z, циркулируя таким же образом, как ток I в петле (фиг. 14.8).

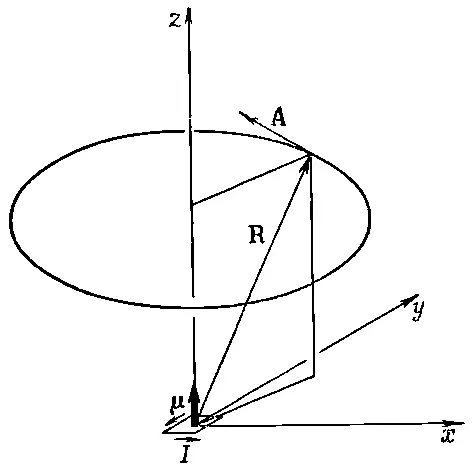
Фиг. 14.8. Векторный потенциал маленькой петли с током, расположенной в начале координат (в плоскости ху). Поле магнитного диполя.

Величина Апропорциональна Iab, т . е. току, умноженному на площадь петли. Это произведение называется магнитным дипольным моментом (или часто просто «магнитным моментом») петли. Мы обозначим его через μ:

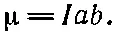(14.32)

Векторный потенциал маленькой плоской петельки любой формы (круг, треугольник и т. п.) также дается уравнениями (14.30) и (14.31), если заменить I ab на

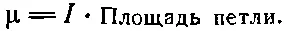(14.33)

Мы предоставляем вам право это доказать.

Нашему уравнению можно придать векторную форму, если определить вектор μ как нормаль к плоскости петли с положительным направлением, определяемым по правилу правой руки (см. фиг. 14.8). Тогда можно написать

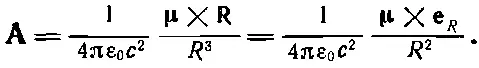(14.34)

Нам еще нужно найти В. Пользуясь (14.33) и (14.34), а также (14.4), получаем

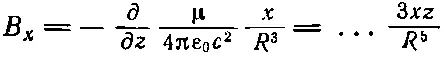(14.35)

(под многоточием мы подразумеваем μ/4πε 0с 2),

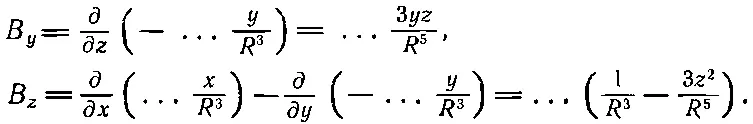
Компоненты поля Введут себя точно так же, как компоненты поля Е для диполя, ориентированного вдоль оси z [см. уравнения (6.14) и (6.15), а также фиг. 6.5, стр. 115]. Вот почему мы называем петлю магнитным диполем. Слово «диполь» в применении к магнитному полю немного запутывает, потому что нет отдельных магнитных «полюсов», соответствующих электрическим зарядам. Магнитное «дипольное поле» создается не двумя «зарядами», а элементарной петлей с током.

В общем-то довольно любопытно, что, начав с совсем разных законов, ∇· Е=ρ/ε 0и ∇× В=j/ε 0с 2, можно прийти к полю одного и того же вида. Почему так получается? Потому что дипольные поля возникают, только когда мы находимся далеко от всех токов и зарядов. Тогда в большей части пространства уравнения для Еи Водинаковы: у обоих дивергенция и ротор равны нулю. Следовательно, они дают одни и те же решения. Однако источники , конфигурацию которых мы описываем с помощью дипольных моментов, физически совершенно различны. В одном случае это циркулирующий ток, а в другом — пара зарядов, один над, а другой под плоскостью петли для соответствующего поля.

Нас часто интересует магнитное поле, создаваемое цепью проводов, в которой диаметр провода очень мал по сравнению с размерами всей системы. В таких случаях мы можем упростить уравнения для магнитного поля.