Ричард Фейнман - Том 2. Электромагнетизм и материя

Для тонкого провода элемент объема можно записать в виде

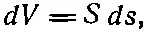
где S — площадь поперечного сечения провода, а d s— элемент расстояния вдоль проволоки. В самом деле, поскольку вектор d sимеет то же направление, что и j(фиг. 14.9), и мы можем предположить, что jпостоянно по любому данному сечению, то можно записать векторное уравнение

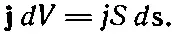(14.37)

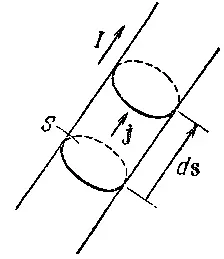
Фиг. 14.9. Для тонкой проволоки jdV то же самое, что и Ids.

Ho jS — как раз то, что мы называем током I во всем проводе, так что наш интеграл для векторного потенциала (14.19) становится равным

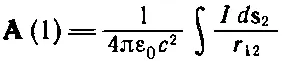(14.38)

(фиг. 14.10).

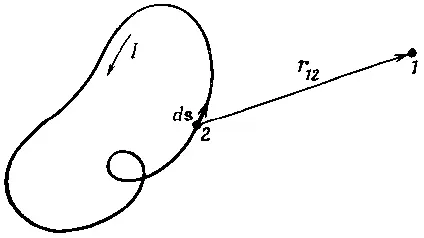
Фиг. 14.10. Магнитное поле провода может быть получено интегрированием по всей цепи.

(Мы предполагаем, что I одно и то же вдоль всего контура. Если есть несколько ответвлений с разными токами, то следует, конечно, брать соответствующий ток в каждой ветви.)

Как и раньше, можно найти поле с помощью (14.38) либо прямым интегрированием, либо решая соответствующую электростатическую задачу.

В ходе изучения электростатики мы нашли, что электрическое поле известного распределения зарядов может быть получено сразу в виде интеграла [уравнение (4.16)]

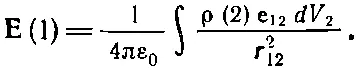
Как мы видели, вычислить этот интеграл (а их на самом деле три, по одному на каждую компоненту) обычно бывает труднее, чем вычислить интеграл для потенциала и взять от него градиент.

Подобный интеграл связывает и магнитное поле с токами. Мы уже имеем интеграл для А[уравнение (14.19)]; мы можем получить интеграл и для В, если возьмем ротор от обеих частей:

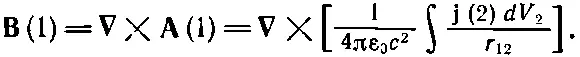
А теперь мы должны быть осторожны. Оператор ротора означает взятие производных от А(1), т. е. он действует только на координаты (x 1, y 1, z 1). Можно внести оператор ∇× под интеграл, если помнить, что он действует только на переменные со значком 1, которые появляются, конечно, только в

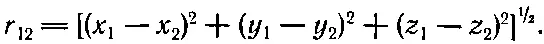
Мы получаем для x-компоненты В:

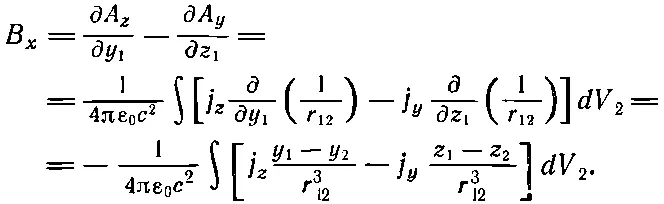(14.41)

Величина в скобках есть просто x-компонента от

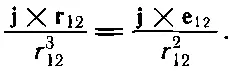
Такие же результаты получаются и для других компонент, и мы имеем

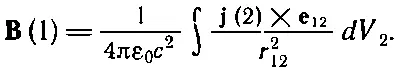(14.42)

Интеграл дает Всразу через известные токи. Геометрия здесь точно такая же, какая изображена на фиг. 14.2.

Если токи текут только по тонким проводам, мы можем, как в предыдущем параграфе, немедленно взять интеграл поперек провода, заменив j dV на I ds , где d s — элемент длины провода. Тогда, пользуясь обозначениями фиг. 14.10, имеем

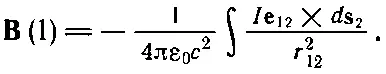(14.43)

(Знак минус появляется потому, что мы изменили порядок векторного произведения.) Это уравнение для В называется законом Био — Савара в честь открывших его ученых. Он дает формулу для прямого вычисления магнитного поля, создаваемого проводами с током.

Вероятно, вы удивились: «Какой же прок от векторного потенциала, если мы можем сразу найти Вв виде векторного интеграла? В конце концов Атоже определяется тремя интегралами!» Из-за векторного произведения интегралы для Вобычно сложнее устроены, как это видно из уравнения (14.41). Кроме того, поскольку интегралы для Апохожи на электростатические, то нам не надо их вычислять заново. Наконец, мы увидим, что в более трудных теоретических вопросах, таких, как теория относительности, в современном изложении законов механики, вроде принципа наименьшего действия, о котором будет рассказано позже, в квантовой механике, векторный потенциал играет важную роль.

В предыдущей главе мы изучали магнитное поле, создаваемое маленькой прямоугольной петлей, по которой течет ток. Мы нашли, что это поле диполя с дипольным моментом, равным

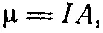(15.1)

где I — сила тока, а A — площадь петли. Момент направлен по нормали к плоскости петли, так что можно писать и так:

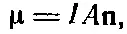
где n— единичный вектор нормали к площади А .

Петли с током, или магнитные диполи, не только создают магнитные поля, но и сами подвергаются действию силы, попав в магнитное поле других токов. Рассмотрим сперва силы, действующие на прямоугольную петлю в однородном магнитном поле. Пусть ось z направлена по полю, а ось y лежит в плоскости петли, образующей с плоскостью xy угол θ (фиг. 15.1). Тогда магнитный момент петли, будучи нормальным к ее плоскости, образует с магнитным полем тоже угол θ.

Раз токи на противоположных сторонах петли текут в противоположные стороны, то и силы, действующие на них, тоже направлены врозь, а суммарная сила равна нулю (в однородном поле). Но благодаря силам, действующим на стороны, обозначенные на фиг. 15.1 цифрами 1 и 2, возникает вращательный момент, стремящийся вращать петлю вокруг оси у .

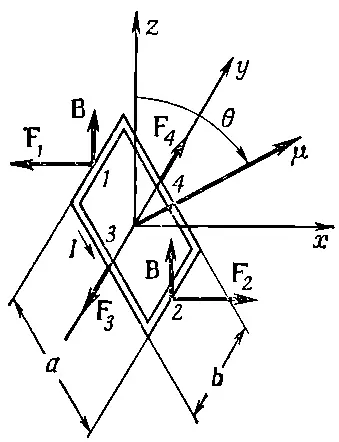
Фиг. 15.1. Прямоугольная петля с током I в однородном поле В, направленном по оси z. Действующий на нее вращательный момент равен τ=μ×B, где магнитный момент μ=Iab.