Ричард Фейнман - Том 2. Электромагнетизм и материя

Теперь предположим, что мы смотрим на происходящее с другой точки зрения: будем считать, что петля покоится, а катушка приближается к ней. Тогда катушка движется в поле, созданном петлей. Те же рассуждения приведут к выражению

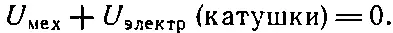
Механическая энергия в обоих случаях одна и та же — она определяется только силой, действующей между двумя контурами.

Сложение двух уравнений дает

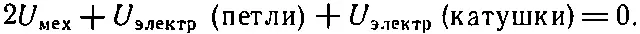
Полная энергия всей системы равна, конечно, сумме двух электрических энергий и взятой один раз механической энергии. В итоге выходит

(15.13)

Полная энергия всей системы — это на самом деле U мех со знаком минус . Если нам нужна, скажем, полная энергия магнитного диполя, то следует писать

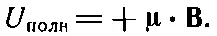
И только тогда, когда мы потребуем, чтобы все токи оставались постоянными, можно использовать лишь одну из частей энергии U мех(всегда равную истинной энергии со знаком минус) для вычисления механических сил. В более общих задачах надо соблюдать осторожность, чтобы не забыть ни одной из энергий. Сходное положение наблюдалось и в электростатике. Мы показали там, что энергия конденсатора равна Q 2/2 C . Когда мы применяем принцип виртуальной работы, чтобы найти силу, действующую между обкладками конденсатора, то изменение энергии равно Q 2/2, умноженному на изменение в 1/ С , т. е.

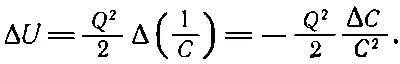(15.14)

А теперь предположим, что нам надо было бы подсчитать работу, затрачиваемую на сближение двух проводников, но при другом условии — что напряжение между ними остается постоянным. Тогда правильную величину силы мы могли бы получить из принципа виртуальной работы, если бы поступили немного искусственным образом. Раз Q = CV , то полная энергия равна 1/ 2 CV 2. Но если бы мы ввели условную энергию, равную — 1/ 2CV 2, то принцип виртуальной работы можно было бы применить для получения сил, полагая изменение этой условной энергии равным механической работе (это при условии, что напряжение V считается постоянным). Тогда

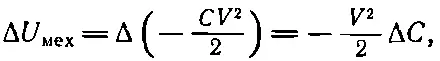(15.15)

а это то же самое, что написано в уравнении (15.14). Мы получаем правильный ответ, хотя пренебрегаем работой, которую электрическая система тратит на постоянное поддержание напряжения. И здесь опять электрическая энергия ровно вдвое больше механической и имеет обратный знак.

Итак, если мы ведем расчет искусственно, пренебрегая тем фактом, что источник потенциала должен тратить работу на то, чтобы напряжение оставалось неизменным, то все равно мы приходим к правильному результату. Это в точности соответствует положению дел в магнитостатике.

Зная, что U полн=-U мех, используем этот факт, чтобы найти истинную энергию постоянных токов в магнитных полях. Начать можно с истинной энергии небольшой токовой петельки. Обозначая U полн просто через U, напишем

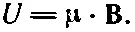(15.16)

Хотя эту энергию мы подсчитали только для плоской прямоугольной петли, все это верно и для плоской петельки произвольной формы.

Энергию контура произвольной формы можно найти, представив себе, что он состоит из небольших токовых петель. Скажем, имеется провод в форме петли Г (фиг. 15.4).

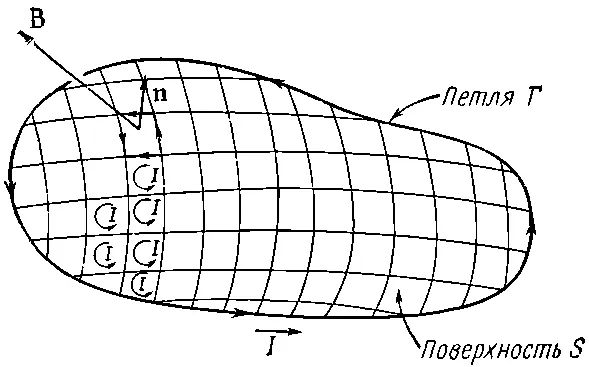
Фиг. 15.4. Энергию большой петли в магнитном поле можно считать суммой энергий маленьких петелек.

Натянем на эту петлю поверхность S , а на ней наметим множество петелек, каждую из которых можно считать плоской. Если заставить ток I циркулировать по каждой петельке, то в итоге выйдет то же самое, как если бы ток шел только по петле Г, ибо токи на всех внутренних линиях взаимно уничтожатся. Система небольших токов физически не будет отличима от исходного контура, и энергия должна быть той же, т. е. должна быть равна сумме энергий всех петелек.

Если площадь каждой петельки Δа, то ее энергия равна IΔаB n, где B n— компонента В , нормальная к Δа. Полная энергия равна

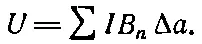
В пределе, когда петли становятся бесконечно малыми, сумма превращается в интеграл, и

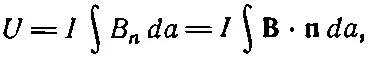(15.17)

где n — единичная нормаль к da .

Если мы положим В= ∇× A, то поверхностный интеграл можно будет связать с контурным (по теореме Стокса):

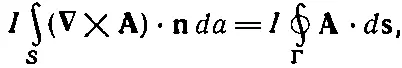(15.18)

где d s— линейный элемент вдоль Г. Итак, мы получили энергию контура произвольной формы:

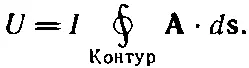(15.19)

В этом выражении Аобозначает, конечно, векторный потенциал, возникающий из-за токов (отличных от тока I в проводе), которые создают поле Вблиз провода.

Далее, любое распределение постоянных токов можно считать состоящим из нитей, идущих вдоль тех линий, по которым течет ток. Для любой пары таких контуров энергия дается выражением (15.19), где интеграл взят вокруг одного из контуров, а векторный потенциал Асоздан другим контуром. Полная энергия получается сложением всех таких пар. Если вместо того, чтобы следить за парами, мы полностью просуммируем по всем нитям, то каждую энергию мы засчитаем дважды (такой же эффект мы наблюдали в электростатике), и полную энергию можно будет представить в виде

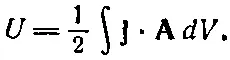(15.20)

Это соответствует полученному для электростатической энергии выражению