Ричард Фейнман - Том 2. Электромагнетизм и материя
- Название:Том 2. Электромагнетизм и материя
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:неизвестен
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Ричард Фейнман - Том 2. Электромагнетизм и материя краткое содержание
Том 2. Электромагнетизм и материя - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
Величина этих сил F 1и F 2такова:
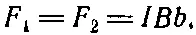
Их плечо равно
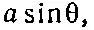
так что вращательный момент
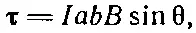
или, поскольку Iab — магнитный момент петли,
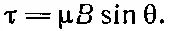
Вращательный момент может быть записан и векторно:
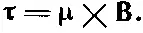 (15.2)
(15.2)
То, что вращательный момент дается уравнением (15.2), мы показали пока только для довольно частного случая. Но результат, как мы увидим, верен для маленьких петель любой формы. Полезно напомнить, что и для вращательного момента, действующего на электрический диполь, мы получили соотношение подобного же рода:
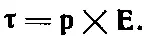
Сейчас нас интересует механическая энергия нашей петли, по которой течет ток. Раз есть момент вращения, то энергия, естественно, зависит от ориентации петли. Принцип виртуальной же работы утверждает, что момент вращения — это скорость изменения энергии с углом, так что можно написать
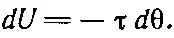
Подставляя τ=+μBsinθ и интегрируя, мы вправе принять за энергию выражение
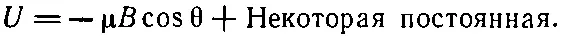 (15.3)
(15.3)
(Знак минус стоит потому, что петля стремится развернуть свой момент по полю; энергия ниже всего тогда, когда μи Впараллельны.)
По причинам, о которых мы поговорим позже, эта энергия не есть полная энергия петли с током. (Мы, к примеру, не учли энергии, идущей на поддержание тока в петле.) Поэтому мы будем называть ее U мех, чтобы не забыть, что это лишь часть энергии. И, кроме того, постоянную интегрирования в (15.3) мы вправе принять равной нулю, все равно ведь какие-то другие виды энергии мы не учли. Так что мы перепишем уравнение так:
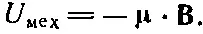 (15.4)
(15.4)
Опять получилось соответствие с электрическим диполем, где было
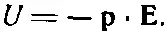 (15.5)
(15.5)
Только в (15.5) электрическая энергия — и вправду энергия, а U мех в (15.4) — не настоящая энергия. Но все равно ее можно применять для расчета сил по принципу виртуальной работы. Надо только предполагать, что ток в петле (или по крайней мере магнитный момент μ) остается неизменным при повороте.
Для нашей прямоугольной петли можно показать, что U мехсоответствует также работе, затрачиваемой на то, чтобы внести петлю в поле. Полная сила, действующая на петлю, равна нулю лишь в однородном поле, а в неоднородном все равно останутся какие-то силы, действующие на токовую петлю. Внося петлю в поле, мы вынуждены будем пронести ее через места, где поле неоднородно, и там будет затрачена работа. Будем считать для упрощения, что петлю вносят в поле так, что ее момент направлен вдоль поля. (А в конце, уже в поле, ее можно повернуть как надо.)
Вообразите, что мы хотим двигать петлю в направлении x, т . е. в ту область, где поле сильнее, и что петля ориентирована так, как показано на фиг. 15.2. Мы отправимся оттуда, где поле равно нулю, и будем интегрировать силу по расстоянию по мере того, как петля входит в поле.
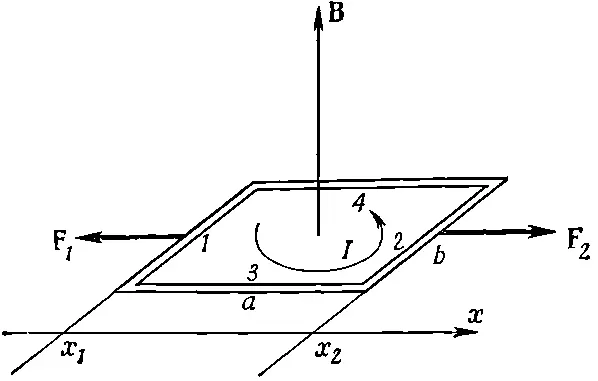
Фиг. 15.2. Петлю проносят через поле В (поперек него) в направлении x.
Рассчитаем сначала работу переноса каждой стороны по отдельности, а затем все сложим (вместо того, чтобы складывать силы до интегрирования). Силы, действующие на стороны 3 и 4, направлены поперек движения, так что на эти стороны работа не тратится. Сила, действующая на сторону 2, направлена по x и равна IbВ ( x ); чтобы узнать всю работу против действия магнитных сил, нужно проинтегрировать это выражение по x от некоторого значения х , где поле равно нулю, скажем, от х =-∞ до теперешнего положения х 2:
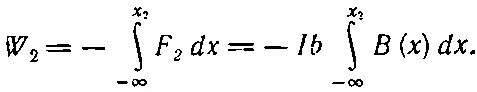 (15.6)
(15.6)
Подобно этому, и работа против сил, действующих на сторону 1, равна
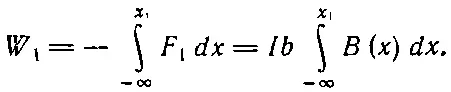 (15.7)
(15.7)
Чтобы вычислить каждый интеграл, надо знать, как В ( х ) зависит от х . Но ведь сторона 1 при движении рамки расположена все время параллельно стороне 2 на одном и том же расстоянии от нее, так что в ее интеграл входит почти вся работа, затраченная на перемещение стороны 2. Сумма (15.6) и (15.7) на самом деле равна
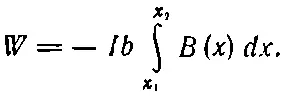 (15.8)
(15.8)
Но, попав в область, где В на обеих сторонах 1 и 2 почти одинаково, мы имеем право записать интеграл в виде
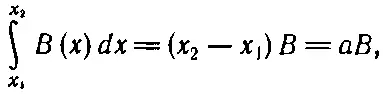
где В — поле в центре петли. Вся вложенная механическая энергия оказывается равной
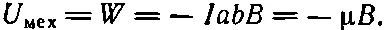 (15.9)
(15.9)
Это согласуется с выражением для энергии (15.4), выбранным нами прежде.
Конечно, тот же вывод получился бы, если бы мы до интегрирования сложили все силы, действующие на петлю. Если бы мы обозначили через В 1поле у стороны 1 а через В 2— поле у стороны 2, то вся сила, действующая в направлении х , оказалась бы равной
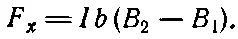
Если петля «узкая», т. е. если В 2и В 1не очень различаются между собой, то можно было бы написать
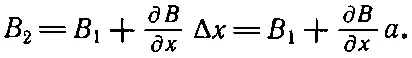
Так что сила была бы равна
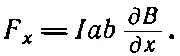 (15.10)
(15.10)
Вся работа, произведенная внешними силами над петлей, равнялась бы
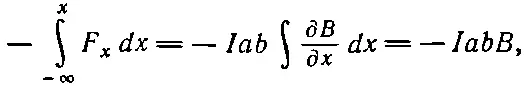
Интервал:
Закладка:






