Ричард Фейнман - Том 3. Квантовая механика

Более того, нам даже не удастся связать эту теорию с некоторыми приближенными формулировками, к которым мы раньше прибегали, скажем, когда изучали молекулу водорода или молекулу аммиака. На этот раз придется бросить дело на полпути, не окончив его. Курс наш близится к концу, и хочешь не хочешь, придется обойтись одним только введением в общие представления. Мы укажем связь с тем, о чем говорилось раньше, и, кроме того, некоторые другие подходы к задачам квантовой механики. Надеемся, что этих представлений вам хватит, чтобы потом двинуться самостоятельно и уже по книгам узнать многие выводы из приведенных здесь уравнений. Все-таки нужно оставить кое-что и на будущее.

Вспомним еще раз, что нам известно о том, как электрон может продвигаться вдоль линии атомов. Когда электрон может с какой-то амплитудой перепрыгивать от одного атома к соседнему, то имеются состояния определенной энергии, в которых амплитуда вероятности обнаружить электрон распределяется вдоль решетки в виде бегущей волны. Для длинных волн (малых значений волнового числа k ) энергия состояния пропорциональна квадрату волнового числа. Для кристаллической решетки с постоянной b , в которой амплитуда того, что электрон в единицу времени перепрыгнет от одного атома к следующему, равна iA / ℏ , энергия состояния связана с k (при малых kb ) формулой

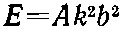(14.1)

(см. гл. 11, § 1). Мы видели также, что группы таких волн с близкими энергиями образуют волновой пакет, который ведет себя как классическая частица с массой m эфф:

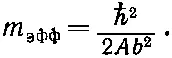(14.2)

Раз волны амплитуды вероятности в кристалле ведут себя как частицы, то естественно ожидать, что общее квантовомеханическое описание частицы выявит такое же волновое поведение, какое мы наблюдали в решетке. Предположим, мы взяли одномерную решетку и вообразили, что постоянная решетки b становится все меньше и меньше. В пределе получилось бы, что электрон может оказаться в любой точке линии. Нам пришлось бы перейти к непрерывному распределению амплитуд вероятности. У электрона появилась бы амплитуда оказаться в любом месте линии. Таков был бы один из путей описания движения электронов в вакууме. Иными словами, если мы вообразим, что все пространство можно пронумеровать бесконечным числом очень тесно расположенных точек, и сможем вывести уравнения, связывающие между собой амплитуды в одной точке с амплитудами в соседних, то получим квантовомеханические законы движения электрона в пространстве.

Начнем с того, что напомним некоторые общие принципы квантовой механики. Пусть имеется частица, которая может в квантовомеханической системе существовать в разных условиях. Любые заданные условия, в которых может быть обнаружен электрон, мы называем «состоянием» и отмечаем их при помощи вектора состояния, скажем |φ>. В каких-то других условиях и метка будет другая, скажем вектор состояния |ψ>. Затем мы вводим идею о базисных состояниях. Мы говорим, что имеется совокупность состояний |1>, |2>, |3>, |4> и т. д., обладающая следующими свойствами. Во-первых, все эти состояния совершенно различны — мы говорим, что они ортогональны. Под этим мы понимаем, что для любой пары базисных состояний | i > и | j > равна нулю амплитуда < i | j > того, что электрон, будучи в состоянии | j >, окажется также и в состоянии < i |, если только, конечно, | i > и | j > не обозначают одного и того же состояния. Все это символически представляется так:

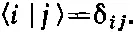(14.3)

Вспомните, что δ ij=0, если i и j различны, и δ ij =1, если i и j одинаковые числа.

Далее, базисные состояния | i > обязаны быть полной совокупностью, так чтобы любое состояние могло быть выражено на их языке. Иначе говоря, любое состояние |φ> может быть полностью описано заданием всех амплитуд < i |φ> того, что частица в состоянии |φ> обнаружится также в состоянии | i >. Вектор состояния |φ> представляется суммой базисных состояний, умноженных каждое на коэффициент, являющийся амплитудой того, что состояние |φ> находится также в состоянии | i >:

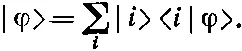(14.4)

Наконец, если рассмотреть любые два состояния |φ> и |ψ>, то амплитуду того, что состояние |ψ> окажется также в состоянии |φ>, можно найти, проецируя сперва состояние |ψ> на базисные состояния, а затем каждое из базисных состояний — на состояние |φ>. Это записывается так:

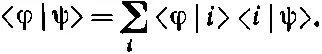(14.5)

Суммирование, конечно, проводится по всей совокупности базисных состояний | i >.

В гл. 11, когда мы рассчитывали, что бывает с электроном, помещенным в линейную цепочку атомов, вы выбрали совокупность базисных состояний, в которых электрон был расположен близ того или иного из атомов цепочки. Базисное состояние | n > представляло электрон, локализованный (расположенный) возле атома номер n . (Конечно, неважно, обозначать ли наши базисные состояния | n > или | i >.) Чуть позже мы нашли, что базисные состояния удобнее метить координатой атома, а не номером атома в цепочке. Состояние | х n > — это просто другой способ записи состояния | n >. Тогда, следуя общему правилу, любое состояние |ψ> можно описать заданием того, что электрон в состоянии |ψ> находится также в одном из состояний | х n >. Для удобства мы решили обозначать эти амплитуды символом

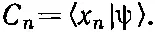(14.6)

Поскольку базисные состояния связаны с местоположением электрона на линии, то амплитуду С n можно рассматривать как функцию координаты х и писать ее в виде С ( х n ). Амплитуды С ( х n ) будут в общем случае меняться во времени и поэтому суть также функции от t , но мы не будем отмечать эту зависимость явно.

Кроме того, в гл. 11 мы предположили, что амплитуды С ( х n ) обязаны меняться во времени так, как положено по гамильтонову уравнению (11.3). В нашем новом обозначении это уравнение имеет вид

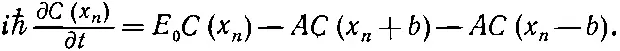(14.7)