Ричард Фейнман - Том 3. Квантовая механика

Вот если бы вы могли определить для каждого из ваших фотонов, какой он — правый или левый и, кроме того , является ли он x -поляризованным (все для одного и того же фотона), то это действительно было бы парадоксом. Но этого вы не сможете сделать — перед вами пример принципа неопределенности.

Если вы все еще не удовлетворены и считаете это «парадоксом», то покажите, что это действительно парадокс: придумайте такой воображаемый опыт, для которого теория квантовой механики двумя различными рассуждениями предсказывала бы два несогласующихся результата. В противном случае «парадокс» — это всего лишь конфликт между тем, что есть на самом деле, и вашим ощущением того, какой «полагалось бы быть» реальной природе.

Вы считаете, что это не «парадокс», но что это все же очень странно? С этим мы все можем согласиться. Именно это и делает физику столь захватывающе интересной.

Сейчас, я надеюсь, вам уже ясно, как важно представление о моменте количества движения для понимания атомных процессов. До сих пор мы рассматривали только системы со спинами (или «полными моментами количества движения») 0, 1/ 2и 1. Но бывают, конечно, и атомные системы с большими моментами количества движения. Для анализа таких систем нужны такие же таблицы амплитуд поворота, какие мы привели в гл. 15, § 6. Иными словами, нужна матрица амплитуд для спина 3/ 2, 2, 5/ 2, 3 и т. д. Мы не будем подробно рассчитывать эти таблицы, но хотели бы показать, как это делается, чтобы вы, если понадобится, могли сами это проделать.

Как мы видели раньше, любая система со спином, или «полным моментом количества движения», j может существовать в одном из 2 j +1 состояний, в которых z-компонента момента количества движения принимает одно из дискретных значений j, j -1, j -2, ..., -( j -1), - j (все в единицах ℏ). Обозначая z-компоненту момента количества движения произвольного выбранного состояния через mℏ , можно определить состояние момента количества движения, задав численные значения двух «квантовых чисел момента количества движения» j и m . Такое состояние можно отметить, указав вектор состояния |j, m >. В случае частиц со спином 1/ 2могут быть два состояния | 1/ 2, 1/ 2> и | 1/ 2, - 1/ 2> a состояния системы со спином 1 в этих обозначениях можно записать как |1, +1>, |1, 0>, |1, -1>. У частицы со спином 0 может быть, конечно, лишь одно состояние |0, 0>.

Теперь мы можем посмотреть, что происходит, когда мы проецируем общее состояние | j, m > на представление, относящееся к повернутой системе осей. Прежде всего известно, что j — это число, которое характеризует систему , поэтому оно не меняется. При повороте осей мы получим просто смесь различных значений m для одного и того же j . В общем случае появится амплитуда того, что система в повернутой системе координат окажется в состоянии | j, m '>, где m ' — новая z-компонента момента количества движения. Значит, нам нужны матричные элементы < j, m ' | R | j, m > всевозможных поворотов. Мы уже знаем, что бывает, если поворот делается на угол φ вокруг оси z . Новое состояние — это попросту старое, умноженное на e im φ, у него по-прежнему то же значение т . Это можно записать так:

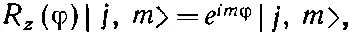(16.24)

или, если вам больше нравится,

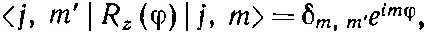(16.25)

(где δ m,m'равно единице при m '= m , и нулю в прочих случаях).

При поворотах вокруг любой другой оси возникает перемешивание различных m -состояний. Можно было бы, конечно, попытаться подсчитать матричные элементы для произвольных поворотов, описываемых углами Эйлера β,α и γ. Но будет легче, если мы вспомним, что самый общий такой поворот может быть составлен из трех поворотов R z (γ), R y (α), R z (β); так что если мы знаем матричные элементы для поворотов вокруг оси y , то уже располагаем всем необходимым.

Как же нам найти матрицу поворота для поворота частицы со спином j на угол θ вокруг оси у ? Опираясь на основные законы (и на то, что уже было), это сделать нелегко. Мы так поступали со спином 1/ 2: вывели все, что нужно, пользуясь довольно сложными соображениями симметрии. Для спина 1 мы это проделали уже иначе: рассмотрели частный случай, когда система со спином 1 складывается из двух систем со спином 1/ 2. Если вы последуете за нами и признаете правильным тот факт, что в общем случае ответы зависят только от спина j , а не от того, как скреплены между собой разные части системы со спином j , то мы сможем обобщить рассуждения для спина 1 на произвольный спин. Мы сможем, например, соорудить искусственную систему со спином 3/ 2из трех объектов со спином 1/ 2. Мы сможем даже избежать всяких усложнений, вообразив, что все они суть различные частицы — скажем, протон, электрон и мюон. Преобразуя каждый объект со спином 1/ 2, мы увидим, что происходит со всей системой — надо только вспомнить, что для комбинированного состояния все амплитуды перемножаются. Давайте посмотрим, как все это проходит.

Допустим, мы расположили все три объекта со спином 1/ 2спинами вверх; обозначим такое состояние |+++>. Если мы взглянем на него из системы координат, повернутой относительно оси z на угол φ, то каждый плюс останется плюсом, но умножится на е i φ/2. Таких множителей у нас тройка, так что

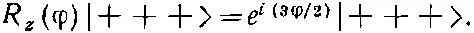(16.26)

Ясно, что состояние |+++> — это как раз то, что мы называем состоянием m =+ 3/ 2, или состоянием | 3/ 2, + 3/ 2>.

Если мы затем повернем эту систему вокруг оси у , то у каждого из объектов со спином 1/ 2появится некоторая амплитуда стать плюсом или стать минусом, так что вся система станет теперь смесью восьми возможных комбинаций |+++>, |++->, |+-+>, |-++>, |+-->, |-+->, |--+> или |--->. Ясно, однако, что их можно разбить на четыре группы, чтобы каждая соответствовала своему значению m . Прежде всего мы имеем |+++>, для которого m = 3/ 2. Затем имеется тройка состояний |++->, |+-+> и |-++> — каждое с двумя плюсами и одним минусом. Поскольку каждый из объектов со спином 1/ 2имеет равные шансы стать после поворота минусом, то каждая из этих трех комбинаций должна войти на равных паях. Поэтому возьмем комбинацию

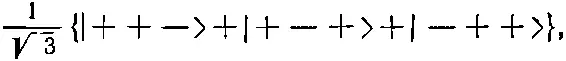(16.27)