Ричард Фейнман - Том 3. Квантовая механика
- Название:Том 3. Квантовая механика
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:неизвестен
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Ричард Фейнман - Том 3. Квантовая механика краткое содержание
Том 3. Квантовая механика - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
где множитель 1/√3 поставлен для нормировки. Если мы повернем это состояние вокруг оси z , то получим множитель e i φ/2для каждого плюса и e - i φ/2для каждого минуса. Каждое слагаемое в (16.27) умножится на e i φ/2, и общий множитель е i φ/2мы вынесем за скобки. Такое состояние соответствует нашему представлению о состоянии с m =+ 1/ 2; мы приходим к выводу, что
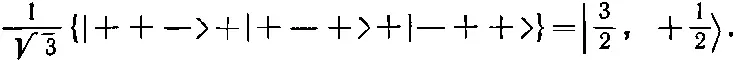 (16.8)
(16.8)
Точно так же можно написать
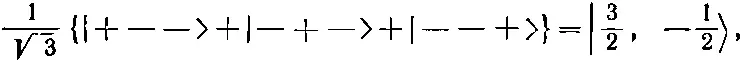 (16.29)
(16.29)
что соответствует состоянию с m =- 1/ 2. Заметьте, что мы берем только симметричные сочетания, у нас нет комбинаций, куда входят слагаемые со знаком минус. Они отвечали бы состояниям с таким же m , но с иным j . Это аналогично случаю спина 1, где (1/√2){|+->+|-+>} было состоянием |1,0>, а (1/√2){|+->-|-+>} было состоянием |0,0>. Наконец, мы имеем
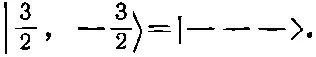 (16.30)
(16.30)
Эта четверка состояний сведена в табл. 16.1.
Таблица 16.1. СВОДКА СОСТОЯНИЙ
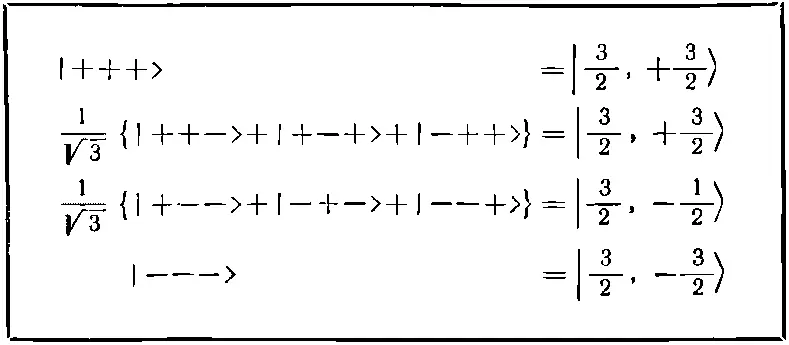
Все, что нам теперь нужно сделать, это взять каждое состояние, повернуть его вокруг оси у и посмотреть, сколько новых состояний оно создаст — пользуясь известной нам матрицей поворота для частицы спина 1/ 2. Можно поступать так же, как мы это делали в случае спина 1 [см. гл. 10, § 6 (вып. 8)]. (Только алгебры будет побольше.) Мы будем строго следовать идеям гл. 10 (вып. 8), так что подробных объяснений давать не будем. Состояния в системе S будут обозначаться
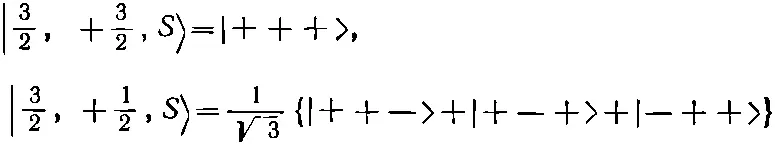
и т. д.; T -системой будет считаться система, повернутая вокруг оси у системы S на угол θ. Состояния в T -системе будут обозначаться | 3/ 2, + 3/ 2, T >, | 3/ 2, + 1/ 2, T > и т. д. Ясно, что | 3/ 2, + 3/ 2, T > это то же самое, что |+'+'+'> (штрихи всегда относятся к T -системе). Точно так же | 3/ 2, + 1/ 2, T > будет равняться
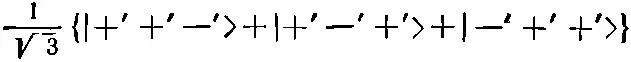
и т. д. Каждое |+'>-состояние в T -системе получается как из |+>-, так и из |->-состояний в системе S с помощью матричных элементов из табл. 10.4 (вып. 8).
Если мы имеем тройку частиц со спином 1/ 2, то (10.47) надо заменить на
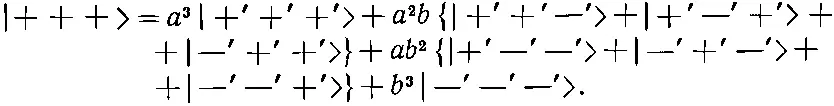 (16.31)
(16.31)
Пользуясь обозначениями табл. 10.4, получим вместо (10.48) уравнение
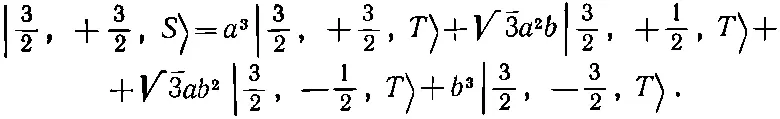 (16.32)
(16.32)
Это уже дает нам некоторые из наших матричных элементов < jT | iS >. Чтобы получить выражение для | 3/ 2, + 1/ 2, S >, мы должны исходить из преобразования состояния с двумя плюсами и одним минусом. К примеру,
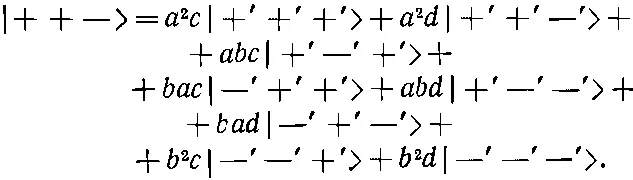 (16.33)
(16.33)
Добавляя два сходных выражения для |+—+> и |—++> и деля на √3, найдем
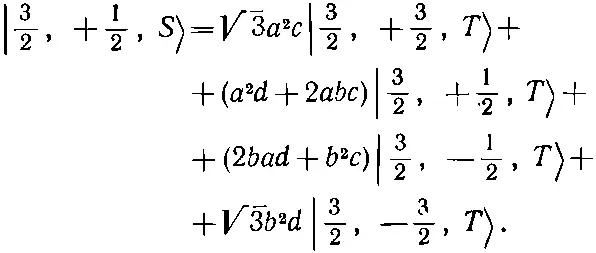 (16.34)
(16.34)
Продолжая этот процесс, мы найдем все элементы < jT | iS > матрицы преобразования. Они приведены в табл. 16.2. Первый столбец получается из (16.32), второй — из (16.34). Последние два столбца были вычислены таким же способом.
Теперь допустим, что T -система была повернута относительно S -системы на угол θ вокруг ее оси у . Тогда а, b, с и d равны [см. (10.54), вып. 8]: а = d =cosθ/2, с =- b =sinθ/2. Подставляя это в табл. 16.2, получаем формулы, похожие на вторую половину табл. 15.2, но на этот раз для системы со спином 3/ 2.
Таблица 16.2. МАТРИЦА ПОВОРОТА ДЛЯ ЧАСТИЦЫ СО СПИНОМ 3/ 2
Коэффициенты а, b, с и d объясняются в табл. 10.4.
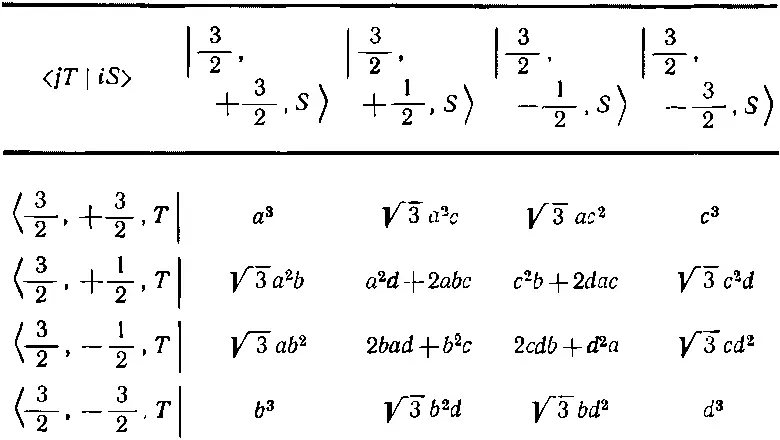
Рассуждения, которые мы только что провели, были обобщены на систему с произвольным спином j . Состояния | j, m > можно составить из 2 j частиц со спином 1/ 2у каждой. (Из них j + m будут в |+>-состоянии, а j - m будут в |->-состоянии.) Проводится суммирование по всем возможным способам, какими их можно сочетать, а затем состояния нормируются умножением на надлежащую постоянную. Если у вас есть способности к математике, то вы сможете доказать, что получается следующий результат [75] Детали вы найдете в добавлении, стр. 165.
:
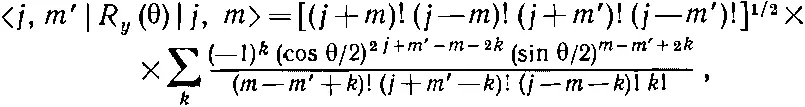 (16.35)
(16.35)
где k пробегает все те значения, при которых под знаком факториала получаются неотрицательные величины.
Это очень запутанная формула, но с ее помощью вы сможете проверить табл. 15.2 для j =1 и составить ваши собственные таблицы для больших j . Некоторые матричные элементы очень важны и получили особые наименования. Например, матричные элементы для m = m '=0 и целых j известны под названием полиномов Лежандра и обозначаются
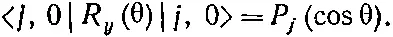 (16.36)
(16.36)
Первые из них таковы:
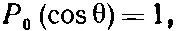 (16.37)
(16.37)
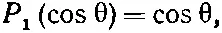 (16.38)
(16.38)
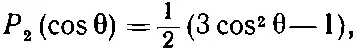 (16.39)
(16.39)
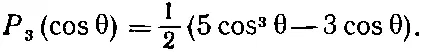 (16.40)
(16.40)
§ 5. Измерение ядерного спина
Продемонстрируем теперь пример, где понадобятся только что описанные коэффициенты. Он связан с проделанными не так давно интересными опытами, которые вы теперь в состоянии будете понять. Некоторым физикам захотелось узнать спин одного из возбужденных состояний ядра Ne 20. Для этого они принялись бомбить углеродную мишень пучком ускоренных ионов углерода и породили нужное им возбужденное состояние Ne 20(обозначаемое Ne 20*) в реакции
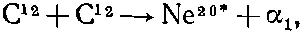
Интервал:
Закладка:






