Ричард Фейнман - Том 3. Квантовая механика

где α 1— это α-частица, или Не 4. Кое-какие из создаваемых таким образом возбужденных состояний Ne 20неустойчивы и распадаются таким путем:

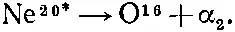
Значит, на опыте видны возникающие в реакции две α-частицы. Обозначим их α 1и α 2; поскольку они вылетают с разными энергиями, их можно отличить друг от друга. Кроме того, выбирая α 1, имеющие нужную энергию, мы можем отобрать любые возбужденные состояния Ne 20.

Опыт ставился так, как показано на фиг. 16.9.

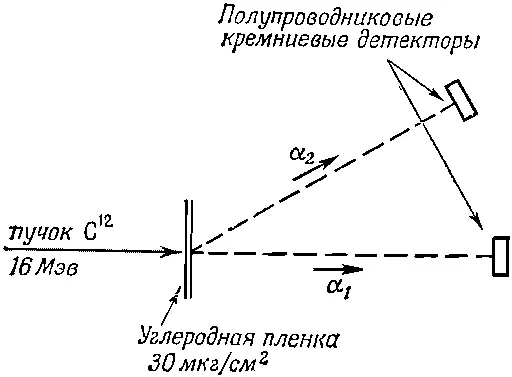
Фиг. 16.9. Размещение приборов в опыте по определению спина возбужденных состояний Ne 20 .

Пучок ионов углерода с энергией 16 Мэв был направлен на углеродную пленку. Первая α-частица регистрировалась кремниевым детектором, настроенным на прием α-частиц с нужной энергией, движущихся вперед (по отношению к падающему пучку ионов С 12). Вторая α-частица регистрировалась счетчиком α 2, поставленным под углом θ к α 1. Скорость счета сигналов совпадений от α 1и α 2измерялась как функция угла θ.

Идея опыта в следующем. Прежде всего нужно знать, что спины С 12, О 16и α-частицы все равны нулю. Назовем направление движения начальных частиц С 12направлением +z; тогда известно, что Ne 20*должен обладать нулевым моментом количества движения относительно оси z . Ведь ни у одной из остальных частиц нет спина; кроме того, С 12прилетает вдоль оси z и α 1улетает вдоль оси z, так что у них не может быть момента относительно этой оси. И каким бы ни был спин j ядра Ne 20*, мы знаем, что это ядро находится в состоянии | j , 0>. Что же случится, когда Ne 20*распадется на О 16и другую α-частицу? Что ж, α-частицу поймает счетчик α 2, а О 16, чтобы сохранить начальный импульс, вынужден будет уйти в противоположную сторону [76] Отдачей, которую испытал Ne 20* в первой реакции, можно пренебречь. Или, еще лучше, подсчитать и сделать поправку на нее. . Относительно новой оси (оси α 2) не может быть тоже никакой компоненты момента количества движения. А раз конечное состояние имеет относительно новой оси нулевой момент количества движения, то у распада Ne 20*должна быть некоторая амплитуда того, что m '=0, где m '—квантовое число компоненты момента количества движения относительно новой оси. Вероятность наблюдать α 2под углом θ будет на самом деле равна квадрату амплитуды (или матричного элемента)

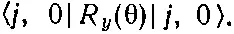(16.41)

Чтобы получить спин интересующего нас состояния Ne 20*, вычертим интенсивность наблюдений второй α-частицы как функцию угла и сравним с теоретическими кривыми для различных значений j . Как мы отмечали в конце предыдущего параграфа, амплитуды < j ,0| R y (θ)| j ,0>—это просто функции Р j (cosθ). Значит, угловые распределения будут следовать кривым [ P j (cosθ)] 2. Экспериментальные результаты для двух возбужденных состояний показаны на фиг. 16.10.

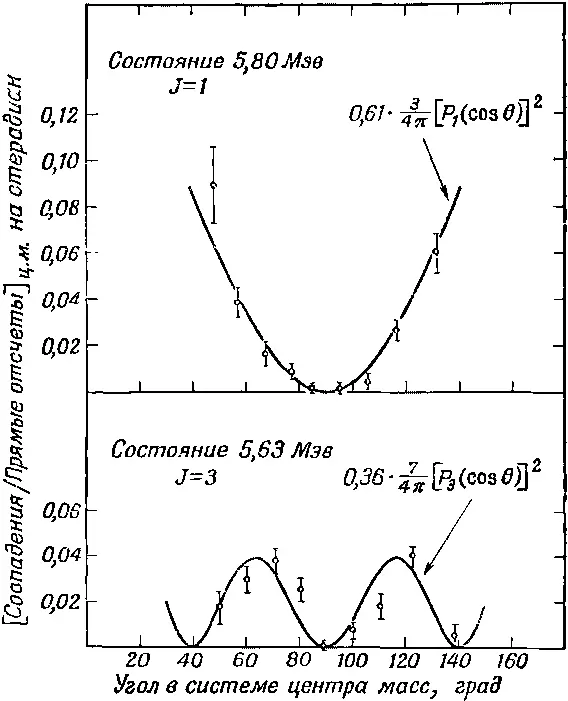
Фиг. 16.10. Экспериментальные результаты измерений углового распределения α-частиц, вылетающих при распаде двух возбужденных состояний Ne 20 . Они получены на устройстве, показанном на фиг. 16.9.

Вы видите, что угловое распределение для состояния 5,80 Мэв очень хорошо укладывается на кривую [ Р 1(cosθ)] 2, т. е. оно должно быть состоянием со спином 1. С другой стороны, данные для состояния 5,63 Мэв выглядят совершенно иначе; они ложатся на кривую [ Р 3(cosθ)] 2. Спин этого состояния равен 3.

В этом опыте мы измерили момент количества движения двух возбужденных состояний Ne 20*. Этой информацией можно воспользоваться, чтобы понять, как ведут себя протоны и нейтроны внутри этого ядра, и это принесет нам добавочные сведения о таинственных ядерных силах.

Когда мы изучали сверхтонкую структуру атома водорода в гл. 10 (вып. 8), нам пришлось рассчитывать внутренние состояния системы, составленной из двух частиц — электрона и протона — со спинами 1/ 2. Мы нашли, что четверка возможных спиновых состояний такой системы может быть разбита на две группы — на тройку состояний с одной энергией, которая во внешнем поле выглядела как частица со спином 1, и на одно оставшееся состояние, которое вело себя как частица со спином 0. Иначе говоря, объединяя две частицы со спином 1/ 2, можно образовать систему, «полный спин» которой равен либо единице, либо нулю. В этом параграфе мы хотим рассмотреть на более общем уровне спиновые состояния системы , составленной из двух частиц с произвольными спинами. Это другая важная проблема, связанная с моментами количества движения квантовомеханической системы.

Перепишем сперва результаты гл. 10 для атома водорода в форме, которая позволит распространить их на более общий случай. Мы начали с двух частиц, которые теперь обозначим так: частица а (электрон) и частица b (протон). Спин частицы а был равен j a (= 1/ 2), а z-компонента момента количества движения m а могла принимать одно из нескольких значений (на самом деле два, а именно m а =+ 1/ 2или m а =- 1/ 2). Точно так же спиновое состояние частицы b описывалось ее спином j b и z-компонентой момента количества движения m b . Из всего этого можно было составить несколько комбинаций спиновых состояний двух частиц. Например, из частицы а с m а = 1/ 2и частицы b с m b =- 1/ 2можно было образовать состояние |а, + 1/ 2; b , - 1/ 2>. Вообще, объединенные состояния образовывали систему, у которой «спин системы», или «полный спин», или «полный момент количества движения» J мог быть равен либо единице, либо нулю, а z-компонента момента количества движения М могла равняться +1, 0 или -1 при J =1 и нулю при J =0. На этом новом языке формулы (10.41) и (10.42) можно переписать так, как показано в табл. 16.3.

Таблица 16.3. СОСТАВЛЕНИЕ МОМЕНТОВ КОЛИЧЕСТВА ДВИЖЕНИЯ ДВУХ ЧАСТИЦ СО СПИНОМ 1/ 2

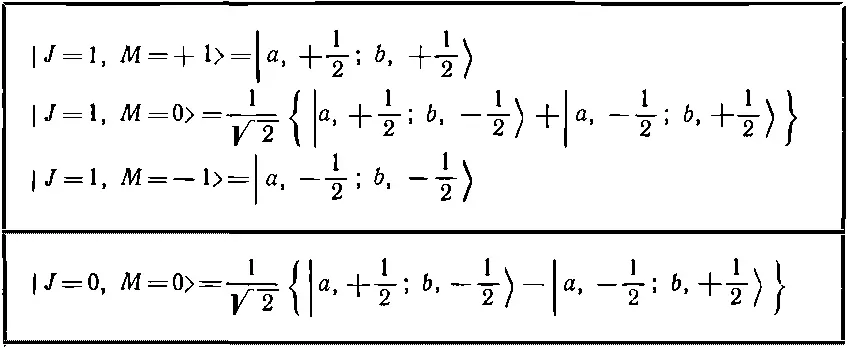
Левый столбец таблицы описывает составное состояние через его полный момент количества движения J и z -компоненту М. Правый столбец показывает, как составляются эти состояния из значений m двух частиц а и b .