Ричард Фейнман - Том 3. Квантовая механика

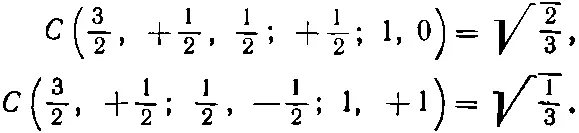
Мы не будем здесь подсчитывать коэффициенты для других частных случаев [77] Тем более, что большая часть работы уже проделана, раз у нас есть общая матрица поворота (16.35). . Но вы обнаружите такие таблицы во многих книжках. Попробуйте сами подсчитать другой случай, например объединение двух объектов со спином 1. Мы же просто привели в табл. 16.7 окончательный результат.

Таблица 16.7. ОБЪЕДИНЕНИЕ ДВУХ ЧАСТИЦ СО СПИНОМ 1 ( j a =1, j b =1)

Эти законы объединения моментов количества движения имеют очень важное значение в физике частиц, их приложениям поистине нет конца. К сожалению, у нас нет сейчас больше времени на другие примеры.

Для тех, кто хотел бы разобраться в этом поподробнее, мы вычислим сейчас общую матрицу поворота для системы со спином (полным моментом количества движения) j . В расчете общего случая на самом деле большой необходимости нет; важно понять идею, а все результаты вы сможете найти в таблицах, которые приводятся во многих книжках. Но, с другой стороны, вы зашли уже так далеко, что у вас, естественно, может возникнуть желание убедиться, что вы и впрямь в состоянии понять даже столь сложные формулы квантовой механики, как (16.35).

Расширим рассуждения § 4 на систему со спином j , которую будем считать составленной из 2 j объектов со спином 1/ 2. Состояние с m = j имело бы вид |+ + + ... +> (с j плюсами). Для m = j -1 было бы 2 j членов типа |+ + ... + + ->, |+ + ... +- +> и т. д. Рассмотрим общий случай, когда имеется r плюсов и s минусов, причем r + s =2 j . При повороте вокруг оси z от каждого из r плюсов появится множитель e + i φ/2. В итоге фаза изменится на i ( r /2- s /2)φ. Мы видим, что

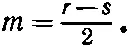(16.59)

Как и в случае J = 3/ 2, каждое состояние с определенным m должно быть суммой всех состояний с одними и теми же r и s , взятых со знаком плюс, т. е. состояний, отвечающих всевозможным перестановкам с r плюсами и s минусами. Мы считаем, что вам известно, что всего таких сочетаний есть (r+s)!/r!s!. Чтобы нормировать каждое состояние, надо эту сумму разделить на корень квадратный из этого числа. Можно написать

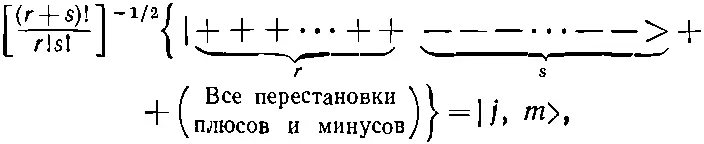(16.60)

где

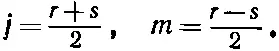(16.61)

Введем еще новые обозначения, они нам помогут в счете. Ну а поскольку мы уж определили состояния при помощи (16.60), то два числа r и s определяют состояние ничуть не хуже, чем j и m . Мы легче проследим за выкладками, если обозначим

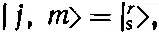(16.62)

где [см.. (16.61)]

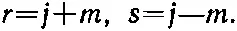
Далее, (16.60) мы запишем, пользуясь специальным обозначением

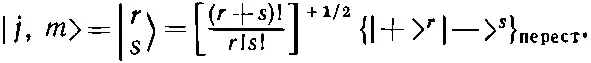(16.63)

Обратите внимание, что показатель степени в общем множителе мы изменили на + 1/ 2. Это оттого, что внутри фигурных скобок в (16.60) стоит как раз N =(r+s)!/r!s! слагаемых. Если сопоставить (16.63) с (16.60), то ясно, что

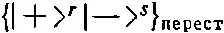
— это краткая запись выражения

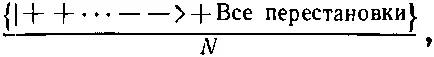
где N — количество различных слагаемых в скобках. Эти обозначения удобны тем, что каждый раз при повороте все знаки плюс вносят один и тот же множитель, так что в итоге он получается в r -й степени. Точно так же все знаки минус дадут некоторый множитель в s -й степени, в каком бы порядке эти знаки ни стояли.

Теперь положим, что мы повернули нашу систему вокруг оси у на угол θ. Нас интересует R y (θ)| r s>. Оператор R y (θ), действуя на каждый |+>, дает

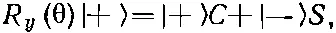(16.64)

где С =cosθ/2 и S =sin θ/2. Когда же R y (θ) действует на |->, это приводит к

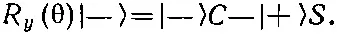
Так что искомое выражение равно

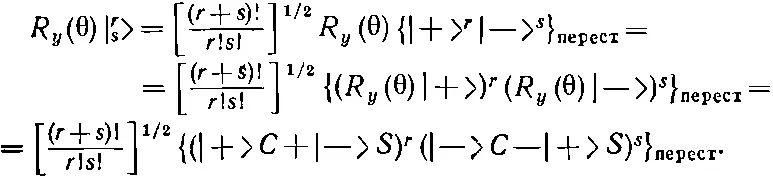(16.65)

Теперь надо возвысить биномы в степень и перемножить. Появятся члены со всеми степенями |+> от нуля до r+s. Посмотрим, какие члены дадут r'-ю степень |+>. Они всегда будут сопровождаться множителем типа |-> s', где s '=2 j - r '. Соберем их вместе. Получится сумма членов типа |+> r'|-> s'с численными коэффициентами А r ', куда входят коэффициенты биномиального разложения вместе с множителями С и S . Уравнение (16.65) тогда будет выглядеть так:

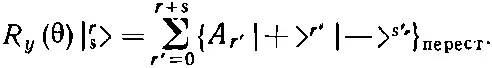(16.66)

Теперь разделим каждое А r 'на множитель [( r '+ s ')!/ r '! s '!] 1/2и обозначим частное через В r . Тогда (16.66) превратится в

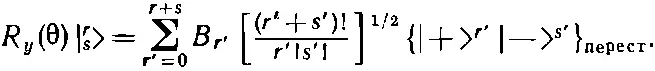(16.67)

[Можно просто сказать, что требование, чтобы (16.67) совпадало с (16.65), определяет B r ']

Если так определить В r ', то оставшиеся множители в правой части (16.67) будут как раз состояниями| r' s'>. Итак, имеем

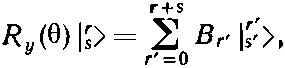(16.68)

где s' всегда равняется r + s - r '. А это, конечно, означает, что коэффициенты В r 'и есть искомые матричные элементы

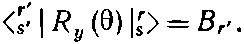(16.69)