Ричард Фейнман - Том 3. Квантовая механика

В этих приближениях амплитуда того, что электрон будет обнаружен в том или ином месте пространства, может быть представлена как функция положения электрона в пространстве и времени. Обозначим амплитуду того, что электрон будет обнаружен в точке х, у, z в момент t через ψ( x, у, z, t ). Согласно квантовой механике, скорость изменения этой амплитуды со временем дается гамильтоновым оператором, действующим на ту же функцию. Из гл. 14 мы знаем, что

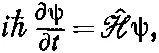(17.1)

где

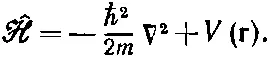(17.2)

Здесь m —масса электрона, а V ( r)— потенциальная энергия электрона в электростатическом поле протона. Считая на больших удалениях от протона V =0, можно написать [79] Как обычно, e 2 = q e 2 /4πε 0

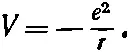
Волновая функция ψ должна тогда удовлетворять уравнению

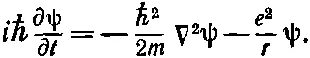(17.3)

Мы хотим найти состояния с определенной энергией, поэтому попробуем поискать решения, которые бы имели вид

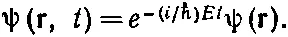(17.4)

Тогда функция ψ( r) должна быть решением уравнения

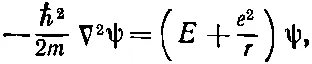(17.5)

где Е — некоторое постоянное число (энергия атома).

Раз потенциальная энергия зависит только от радиуса, то это уравнение лучше решать в полярных координатах.

Лапласиан в прямоугольных координатах определялся так:

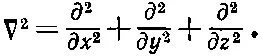
Вместо этого мы хотим воспользоваться координатами r,θ, φ, изображенными на фиг. 17.1.

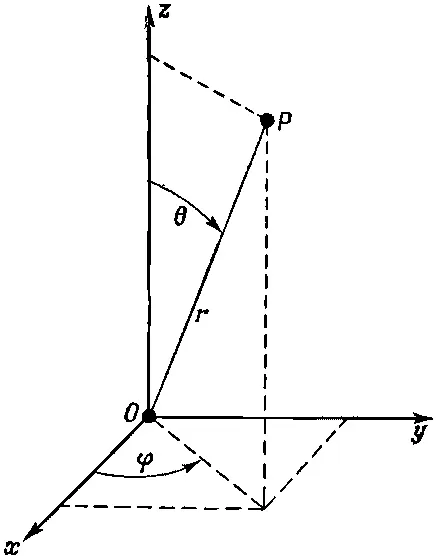
Фиг. 17.1. Сферические координаты r, θ, φ точки Р.

Они связаны с х, у, z формулами

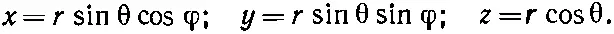
Вас ждут довольно нудные алгебраические выкладки, но в конце концов вы должны будете прийти к тому, что для произвольной функции f (r)= f ( r , θ, φ):

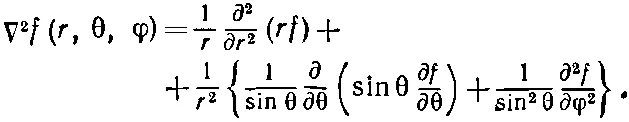(17.6)

Итак, в полярных координатах уравнение, которому должна удовлетворять функция ψ( r , θ, φ), принимает вид

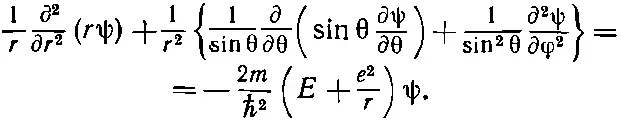(17.7)

Попробуем сперва отыскать какую-нибудь функцию попроще, чтобы она удовлетворяла уравнению (17.7). Хотя волновая функция ψ в общем случае будет зависеть как от θ и φ, так и от r, можно все же поискать, не бывает ли такого особого случая, когда ψ не зависит от углов. Если волновая функция от углов не зависит, то при поворотах системы координат ни одна из амплитуд никак не будет меняться. Это означает, что все компоненты момента количества движения равны нулю. Такая функция ψ должна соответствовать состоянию с равным нулю полным моментом количества движения. (На самом деле, конечно, равен нулю только орбитальный момент количества движения, потому что остается еще спин электрона, но мы на эту часть момента не обращаем внимания.) Состояние с нулевым орбитальным моментом количества движения имеет особое название. Его называют «s-состоянием» (можете считать, что s от слова «сферически симметричный») [80] Поскольку это и другие особые наименования являются частью общепринятого словаря атомной физики, вам попросту придется выучить их. Мы вам поможем их запомнить, поместив в этой главе небольшой «словарик» подобных терминов. .

Раз ψ не собирается зависеть от θ и φ, то в полном лапласиане останется только один первый член и (17.7) сильно упростится:

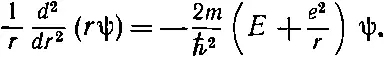(17.8)

Прежде чем заняться решением подобного уравнения, хорошо бы, изменив масштаб, убрать из него все лишние константы вроде е 2, m, ℏ . От этого выкладки станут легче. Если сделать подстановки

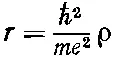(17.9)

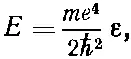(17.10)

то уравнение (17.8) обратится (после умножения на ρ) в

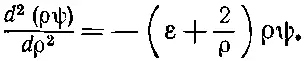(17.11)

Эти изменения масштаба означают, что мы измеряем расстояние r и энергию Е в «естественных» атомных единицах. Например, ρ= r / r B , где r B = ℏ 2/ me 2, называется «боровским радиусом» и равно примерно 0,528 Å. Точно так же ε= E / E R , где E R = me 4/2 ℏ 2. Эта энергия называется «ридбергом» и равна примерно 13,6 эв .

Раз произведение ρψ встречается в обеих частях уравнения, то лучше работать с ним, чем с самим ψ. Обозначив

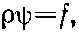(17.12)

мы получим уравнение, которое выглядит проще:

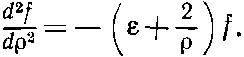(17.13)

Теперь нам предстоит найти функцию f , которая удовлетворяет уравнению (17.13), иными словами, просто решить дифференциальное уравнение. К сожалению, не существует никаких общих, годных во всех случаях жизни методов решения любого дифференциального уравнения. Вы должны просто покрутить его то так, то этак. Хоть уравнение не из легких, но люди все же нашли, что его можно решить при помощи следующей процедуры. Первым делом вы заменяете f , которое является некоторой функцией от ρ, произведением двух функций:

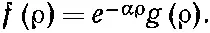(17.14)

Это просто означает, что вы выносите из f (ρ) множитель е -αρ. Для любого f (ρ) это можно сделать. Задача теперь просто свелась к отысканию подходящей функции g (ρ).