Ричард Фейнман - Том 3. Квантовая механика

Подставив (17.14) в (17.13), мы получим следующее уравнение для g :

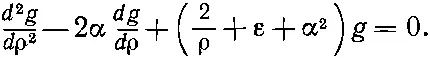(17.15)

Мы вправе выбрать любое α, поэтому сделаем так, чтобы было

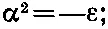(17.16)

тогда получим

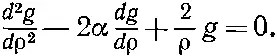(17.17)

Вы можете подумать, что мы не так уж далеко ушли от уравнения (17.13); но новое уравнение тем хорошо, что его можно легко решить разложением g (ρ) в ряд по ρ. В принципе есть возможность таким же способом решать и (17.13), но только все проходит сложнее. Мы говорим: уравнению (17.17) можно удовлетворить некоторой функцией g (ρ), которая записывается в виде ряда

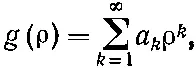(17.8)

где a k— постоянные коэффициенты. И нам осталось только найти подходящую бесконечную последовательность коэффициентов! Проверим, годится ли такая запись решения. Первая производная такой функции g (ρ) равна

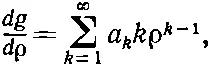
а вторая

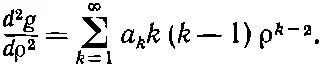
Подставляя это в (17.17), имеем

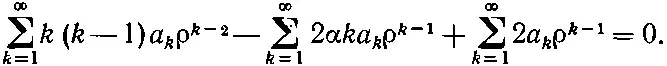(17.19)

Пока еще не ясно, вышло ли у нас что-нибудь; но мы рвемся вперед. Если мы первую сумму заменим некоторым ее эквивалентом, то все выражение станет выглядеть лучше. Первый член в сумме равен нулю, поэтому каждое k можно заменить на k +1, от этого ничего в бесконечном ряде не изменится. Значит, первую сумму мы вправе записать и так:

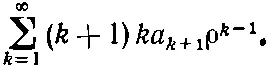
Теперь можно объединить все три суммы в одну:

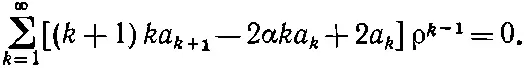(17.20)

Этот степенной ряд должен обращаться в нуль при всех мыслимых значениях ρ, что возможно лишь тогда, когда коэффициенты при каждой степени ρ порознь равны нулю. Мы получим решение для атома водорода, если отыщем такую последовательность a k , для которой

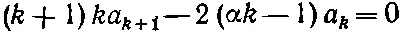(17.21)

при всех k >1. А это, конечно, устроить легко. Выберите какое угодно а 1. Затем все прочие коэффициенты образуйте с помощью формулы

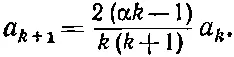(17.22)

Пользуясь ею, вы получите а 2, а 3, а 4и т. д., и каждая пара будет, конечно, удовлетворять (17.21). Мы получим ряд для g (ρ), удовлетворяющий (17.17). С его помощью мы напишем ψ — решение уравнения Шредингера. Обратите внимание, что решения зависят от того, какова предполагаемая энергия (через α), но для каждого значения ε получается свой ряд.

Решение-то у нас есть, но что оно представляет физически? Понятие об этом мы получим, поглядев, что происходит вдалеке от протона — при больших ρ. Там основное значение приобретают наивысшие степени членов ряда, т. е. нам надо посмотреть, что бывает при больших k . Когда k ≫1, то уравнение (17.22) приближенно совпадает с :

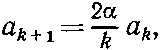
а это означает, что

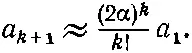(17.23)

Но это как раз коэффициенты разложения в ряд е +2αρ. Функция g оказывается быстро растущей экспонентой. Даже после умножения на е -αρполучающаяся функция f (ρ) [см. (17.14)] будет при больших ρ меняться как е αρ. Мы нашли математическое решение, но оно не является физическим. Оно представляет случай, когда электрону менее всего вероятно очутиться вблизи протона! Чаще всего он вам повстречается на очень больших расстояниях ρ. А волновая функция для связанного электрона должна при больших ρ стремиться к нулю.

Придется подумать, нельзя ли как-нибудь обмануть решение. Оказывается, можно. Посмотрите! Если бы, по счастью, оказалось, что α=1/ n , где n — любое целое число, то уравнение (17.22) привело бы к a n+1=0. И все высшие члены обратились бы тоже в нуль. Вышел бы не бесконечный ряд, а конечный многочлен. Любой многочлен растет медленнее, чем е αρ, поэтому множитель е -αρнаверняка забьет его при больших ρ, и функция f при больших ρ будет стремиться к нулю. Единственные решения для связанных состояний это те, для которых α=1/n, где n =1, 2, 3, 4 и т. д.

Оглядываясь на уравнение (17.16), мы видим, что у сферически симметричного волнового уравнения могут существовать решения для связанных состояний лишь при энергиях

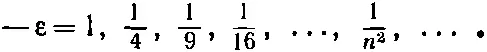
Допустимы только те энергии, которые составляют именно такую часть ридберга Е R = me 4/2 ℏ 2, т. е. энергия n -го уровня равна

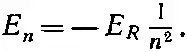(17.24)

Кстати, ничего мистического в отрицательных энергиях нет. Они отрицательны просто потому, что когда мы решили писать V =- е 2/ r , то тем самым в качестве нуля энергии выбрали энергию электрона, расположенного вдалеке от протона. Когда он ближе, то его энергия меньше, т. е. ниже нуля. Энергия ниже всего (самая отрицательная) при n =1 и возрастает к нулю с ростом n .

Еще до открытия квантовой механики экспериментальное изучение спектра водорода показало, что уровни энергии описываются формулой (17.24), где Е R , как это следует из измерений, равно примерно 13,6 э в . Затем Бор придумал модель, которая привела к тому же уравнению (17.24) и предсказала, что E R должно равняться me 4/2 ℏ 2. Первым большим успехом теории Шредингера явилось то, что она смогла воспроизвести этот результат прямо из основного уравнения движения электрона.

Теперь, когда мы рассчитали наш первый атом, давайте рассмотрим свойства полученного нами решения. Объединим все выделившиеся по дороге факторы и выпишем окончательный вид решения: