Ричард Фейнман - Том 3. Квантовая механика

Угловые функции в таблице проходят под несколькими именами и определяются порой с небольшими вариациями в численных множителях, стоящих впереди. Иногда их называют «сферические гармоники» и обозначают Y l,m (θ,φ). Иногда их пишут Р l m (cosθ) e im φ, а при m =0 просто Р l (cosθ). Функции P l ( cos θ) называются «полиномы Лежандра» по cosθ, а функции P l m (cosθ) именуют «присоединенными функциями Лежандра». Таблицы этих функций встречаются во многих книгах.

Обратите, кстати, внимание, что все функции с данным l имеют одну и ту же четность — при нечетных l они от инверсии меняют свой знак, при четных l — нет. Поэтому можно написать, что четность состояния с орбитальным моментом l равна (-1) l .

Как мы видели, одни и те же угловые распределения могут относиться к разным вещам: к ядерному распаду, к другим ядерным процессам, к распределению амплитуд наблюдения электрона в том или ином месте атома водорода. Например, если электрон находится в р -состоянии ( l =1), то амплитуда того, что он обнаружится в каком-то месте, зависит от угла определенным образом, но всегда представляет собой линейную комбинацию трех функций для l =1 из табл. 17.1. Возьмем очень интересный случай cosθ. Он означает, что амплитуда, скажем, положительна в верхней части (θ<���π/2), отрицательна в нижней (θ>π/2) и равна нулю при θ=90°. Возводя ее в квадрат, видим, что вероятность встретить электрон меняется с θ так, как показано на фиг. 17.5, и не зависит от φ.

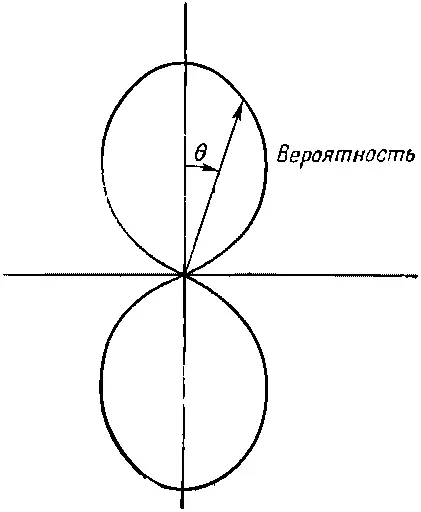
Фиг. 17.5. График cos 2 θ в полярных координатах, дающий относительную вероятность обнаружения электрона под различными углами к оси z (для данного r) в состоянии атома с l=1 и m=0.

Такое угловое распределение ответственно за то, что в молекулярной связи притяжение электрона в состоянии l =1 к другому атому зависит от направления. Отсюда ведет свое начало направленная валентность химического притяжения.

В уравнении (17.35) мы записали волновые функции атома водорода в виде

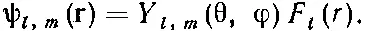(17.37)

Эти волновые функции должны быть решениями дифференциального уравнения (17.7). Посмотрим, что это означает. Подставим (17.37) в (17.7); получим

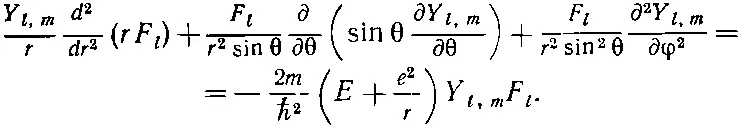(17.38)

Помножим все на r 2/ F l и переставим члены; результат будет таков:

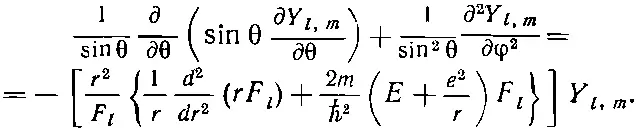(17.39)

Левая часть этого уравнения зависит от θ и φ, а от r не зависит . Какое бы значение r мы ни взяли, от этого левая часть не изменится. Значит, то же должно быть выполнено и для правой части . Хотя в выражении в квадратных скобках там и сям попадаются разные r , все выражение от r зависеть не может, иначе бы не получилось уравнение, которое годится для всех r . Кроме того, как вы видите, эта скобка не зависит ни от θ, ни от φ. Она должна быть постоянным числом. Его величина имеет право зато зависеть от значения l того состояния, которое мы изучаем, поскольку этому состоянию принадлежит функция F l ; поэтому постоянное число мы обозначим K l . Уравнение (17.35), стало быть, равнозначно двум уравнениям

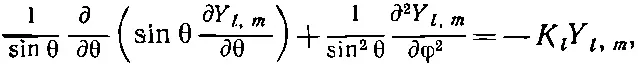(17.40)

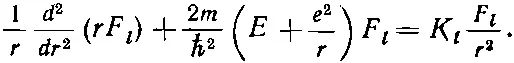(17.41)

Теперь взглянем на то, что мы сделали. Для каждого состояния, описываемого числами l и m , мы знаем функции Y l,m ; тогда из уравнения (17.40) можно определить K l Затем, подставив K l в (17.41), мы получим дифференциальное уравнение для функции F l ( r ). Если мы его сможем решить, то все множители, входящие в (17.37), нам станут известны, и мы узнаем ψ(r).

Чему же равно К l ? Ну, во-первых, заметьте, что при всех m (входящих в данное l ) оно должно быть одним и тем же, поэтому мы вправе выбрать в Y l,m то m , какое нам нравится, и вставить его в (17.40). Пожалуй, проще всего взять Y l,l . Из уравнения (16.24)

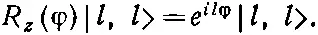(17.42)

Матричный элемент R y (θ) тоже совсем прост:

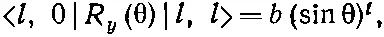(17.43)

где b — некоторое число [81] Это нетрудно вывести из (16.35). Но можно это сделать, исходя из основных принципов; надо только воспользоваться идеями, изложенными в гл. 16, § 4. Состояние |l, l> может быть составлено из 2l частиц со спином 1 / 2 , у которых спин направлен вверх; а в состоянии |l, 0> l спинов было бы направлено вверх, а l — вниз. При повороте амплитуда того, что спин останется тем же, равна cosθ/2, а амплитуда того, что он перевернется, равна sin θ/2. А нас интересует амплитуда того, что l спинов не перевернутся, а другие l перевернутся. Такая амплитуда равна (cosθ/2sinθ/2) l , а это то же самое, что sin l θ. . Объединяя их, получаем

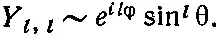(17.44)

Подстановка этой функции в (17.40) даст

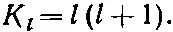(17.45)

Теперь, когда мы определили К l , уравнение (17.41) даст нам радиальную функцию F l ( r ). Перед нами обычное уравнение Шредингера, у которого угловая часть заменена ее эквивалентом K l F l / r 2. Перепишем (17.41) в той форме, в какой мы писали уравнение (17.8):

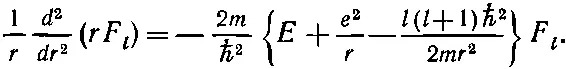(17.46)

У потенциальной энергии появилась какая-то таинственная добавка. Хотя она появилась на свет после длинной серии математических шагов, тем не менее у нее простое физическое происхождение. Мы беремся рассказать о ее происхождении при помощи полуклассических аргументов. После этого она уже не покажется вам такой таинственной.

Представим классическую частицу, вращающуюся вокруг некоторого силового центра. Полная энергия сохраняется и является суммой потенциальной и кинетической энергий