Ричард Фейнман - Том 3. Квантовая механика

Давайте все это распишем. Матрицы преобразования для поворотов мы уже вычислили. Чтобы перейти от системы х, у, z к системе х ', у ', z ' (см. фиг. 17.3), можно сперва сделать поворот вокруг оси z на угол φ, а потом сделать поворот вокруг новой оси у (оси у ') на угол θ. Совместный поворот выразится произведением

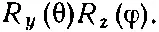
Амплитуда того, что после поворота обнаружится состояние | l, m '=0>, есть

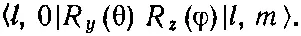(17.31)

В итоге получаем

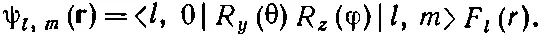(17.32)

Орбитальное движение может обладать только целыми значениями l . (Если электрон может быть обнаружен в любом месте, где r ≠0, то имеется некоторая амплитуда того, что в этом направлении будет m =0. А состояния с m =0 бывают только при целых спинах.) Матрицы поворота для l =1 приведены в табл.15.2. Для больших l вы можете воспользоваться общими формулами, выведенными в гл. 16. Матрицы R z (φ) и R y (θ) написаны по отдельности, но как их комбинировать, вы знаете. В общем случае вы начнете с состояния | l, m > и подействуете на него оператором R z (φ), получив новое состояние R z (φ)| l, m > (которое просто равно e im φ| l, m >). Затем вы подействуете на это состояние оператором R y (θ) и получите состояние R y (θ) R z (φ) | l, m >. Умножение на < l , 0| даст вам матричный элемент (17.31).

Матричные элементы операции поворота — это алгебраические функции от θ и φ. Те частные виды функций, которые появляются в (17.31), возникают и во многих других задачах, связанных с волнами на сфере. Им присвоили особое имя. Правда, не у всех авторов обозначения одинаковы; чаще всего все же пишут

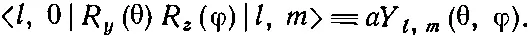(17.33)

Функции Y l,m (θ, φ) называют сферическими гармониками , а a — просто численный множитель, который зависит от того, как определено Y l,m . При обычном определении

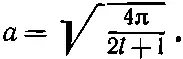(17.34)

В этих обозначениях волновые функции водорода записываются так:

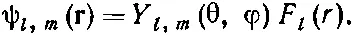(17.35)

Угловые функции Y l,m (θ,φ) важны не только во многих квантовомеханических задачах, но и во многих областях классической физики, в которых встречается оператор ∇ 2, например в электромагнетизме. В качестве другого примера их применения в квантовой механике рассмотрим распад возбужденного состояния Ne 20(о котором говорилось в предыдущей главе), которое испускает α-частицу и превращается в О 16:

Допустим, что возбужденное состояние имеет спин l (обязательно целый), а z -компонента момента количества движения есть т . Спросим вот о чем: если даны l и m , то какова амплитуда того, что α-частица вылетит в направлении, составляющем с осью z угол θ и с плоскостью xz угол φ (фиг. 17.4)?

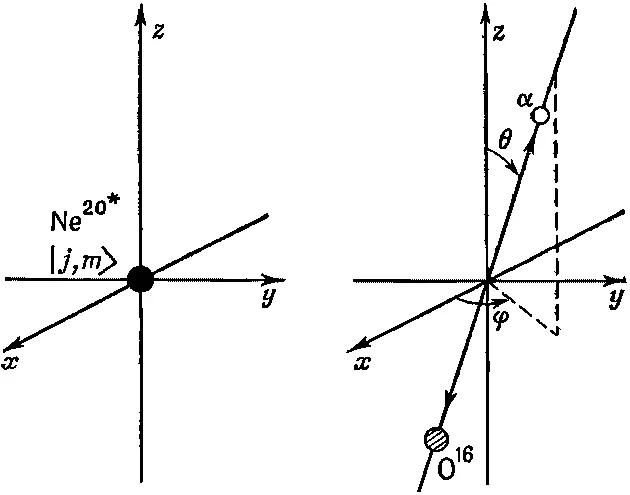
Фиг. 17.4. Распад возбужденного состояния Ne 20 .

Решить эту задачу нам поможет следующее наблюдение. Распад, в котором α-частица вылетает прямо вдоль оси z, должен происходить из состояния с m =0. Это потому, что у самих О 16и α-частицы спин равен нулю, а за счет движения вдоль оси z момента вокруг этой оси не создашь. Обозначим эту амплитуду а (на единицу телесного угла). Тогда, чтобы найти амплитуду распада под произвольным углом (см. фиг. 17.4), остается только узнать, с какой амплитудой данное начальное состояние будет обладать нулевым моментом относительно направления распада. Амплитуда того, что распад будет в направлении (θ, φ), тогда будет равна произведению а на амплитуду того, что состояние | l, m > относительно оси z окажется в состоянии | l , 0> относительно z ' (направления распада). Эта последняя амплитуда как раз и есть то, что мы писали в (17.31). Вероятность увидеть α-частицу под углом (θ, φ), стало быть, равна

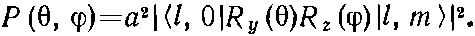
Для примера рассмотрим начальное состояние с l =1 и различными т . Из табл. 15.2 мы знаем все нужные амплитуды:

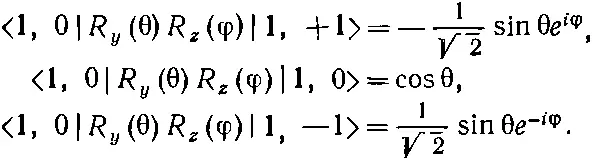(17.36)

Это и есть три возможные амплитуды угловых распределений, в зависимости от того, какое m у первоначального ядра.

Такие амплитуды, как (17.36), встречаются так часто и так важны, что им дали несколько названий. Если амплитуда углового распределения пропорциональна любой из этих трех функций или любой их линейной комбинации, то мы говорим: «орбитальный момент системы равен единице». Или можно сказать: «Ne 20*испускает р -волну». Или говорят: «α-частица испускается в состоянии с l =1». Выражений так много, что даже стоит составить словарик. Если вы хотите понимать разговор физиков, то вам просто нужно выучить их язык. В табл. 17.1 приведен словарь орбитальных моментов количества движения.

Таблица 17.1. СЛОВАРИК ОРБИТАЛЬНЫХ МОМЕНТОВ ( l = j -ЦЕЛЫЕ ЧИСЛА)

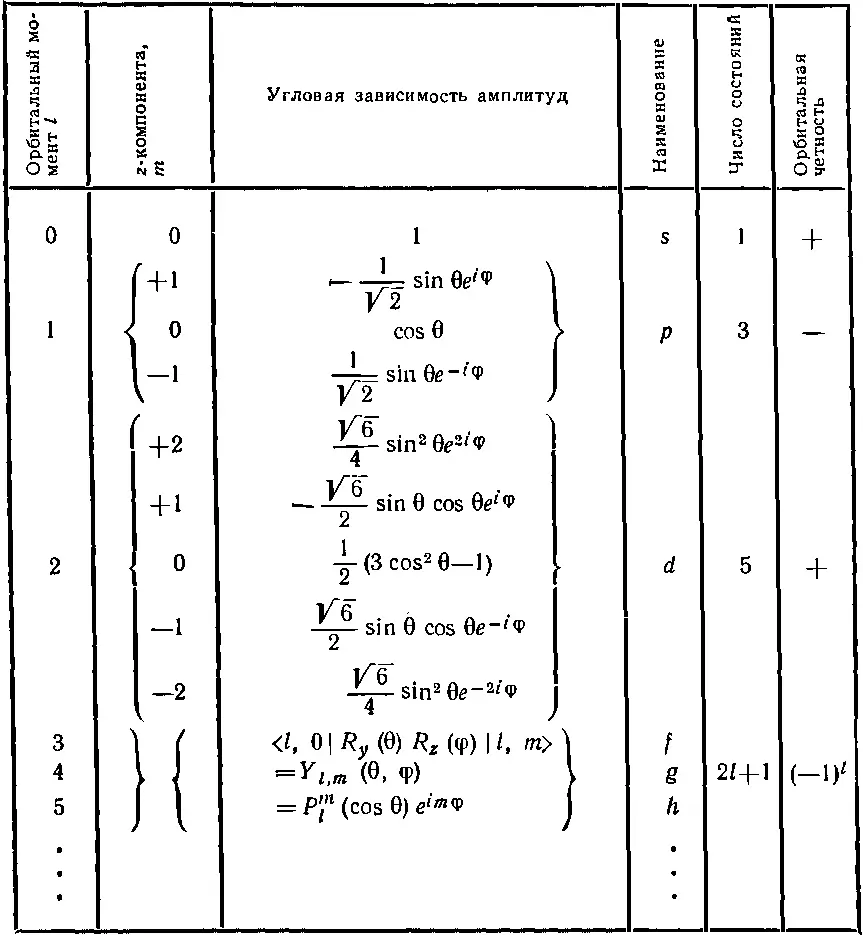
Если орбитальный момент равен нулю, то повороты системы координат ничего не меняют и зависимости от угла нет: «зависимость» от угла имеет вид постоянной, скажем 1. Это называют « s -состоянием». Есть только одно такое состояние, пока дело касается только зависимости от угла. Если орбитальный момент равен 1, то амплитуда зависимости от углов может быть одной из трех приведенных функций, смотря по тому, чему равно m , или их линейной комбинацией. Их называют « р -состояниями». Таких состояний три. Если орбитальный момент равен 2, то подобных функций пять (см. таблицу). Любая их линейная комбинация называется « l =2»-амплитудой, или амплитудой « d -волны». Теперь вы сразу догадаетесь, какая будет следующая буква. Что должно идти после s, p, d ? Ну, конечно же, f, g, h и т. д. по алфавиту. Буквы эти ничего не значат. [Когда-то они что-то значили: «резкая» (sharp), «главная» (principal), «диффузная» (diffuse) и «фундаментальная» (fundamental) серии линий оптического спектра атомов. Но это было тогда, когда еще не было известно, откуда эти серии линий берутся. После f особых названий уже не было, так что мы сейчас просто продолжаем g, h и т. д.]