Ричард Фейнман - Том 3. Квантовая механика

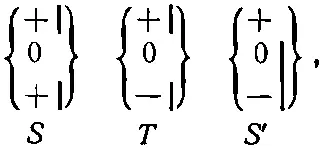(3.12)

в котором изменилось только первое S . Пусть, скажем, угол α (между S и Т ) таков, что в опыте (3.11) треть атомов, прошедших сквозь Т , прошла также и через S '. В опыте (3.12), хоть в нем, вообще говоря, через Т пройдет другое число атомов, но через S ' пройдет та же самая, часть их — одна треть.

Мы можем на самом деле показать, опираясь на то, чему мы научились раньше, что доля атомов, которые выходят из Т и проходят через произвольный определенный фильтр S ', зависит лишь от Т и S ', а не от чего бы то ни было происходившего ранее. Сравним опыт (3.12) с

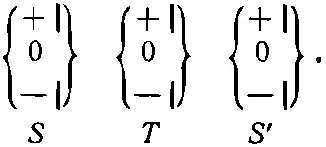(3.13)

Амплитуда того, что атом, выходящий из S , пройдет и сквозь Т , и сквозь 6", в опыте (3.12) равна

Соответствующая вероятность такова:

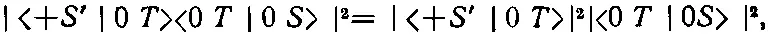
а вероятность в опыте (3.13)

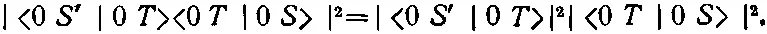
Их отношение

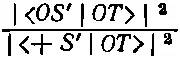
зависит только от Т и S ' и совсем не зависит от того, какой пучок (+ S ), (0 S ) или (- S ) был отобран в S . (Абсолютные же количества могут быть большими или меньшими, смотря по тому, сколько прошло через Т .) Мы бы получили, конечно, аналогичный результат, если бы сравнили вероятности того, что атомы перейдут в плюс- или минус-состояние (по отношению к S '), или отношения вероятностей перейти в нуль- или минус-состояние.

Но раз эти отношения зависят только от того, какой пучок может пройти сквозь Т , а не от отбора, выполненного первым фильтром S , то становится ясно, что тот же результат получился бы, если бы последний прибор даже не был фильтром S . Если в качестве третьего прибора (назовем его R ) мы используем прибор, повернутый относительно Т на некоторый произвольный угол, то все равно увидим, что отношения типа

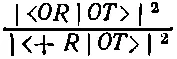
не зависят от того, какой пучок проник через первый фильтр S .

Эти результаты иллюстрируют один из основных принципов квантовой механики: любая атомная система может быть разделена процессом фильтрования на определенную совокупность того, что мы назовем базисными состояниями , и будущее поведение атомов в любом данном отдельном базисном состоянии зависит только от природы базисного состояния — оно не зависит от предыдущей истории [6] Мы не собираемся вкладывать в слова «базисное состояние» что-либо сверх того, что здесь сказано. Не следует переводить «базис» как «основу» и хоть в каком-то смысле считать их «основными состояниями». Слово «базис» понимается как «система описания», скажем, в таком смысле, как в выражении «число в десятичной системе». . Базисные состояния зависят, конечно, от примененного фильтра; например, три состояния (+ Т ), (0 Т ) и (- Т )—это одна совокупность базисных состояний, а три состояния (+ S ), (0 S ) и (- S ) — другая. Возможностей сколько угодно, и ни одна не хуже другой.

Необходимо быть осторожным, утверждая, что мы рассматриваем хорошие фильтры, которые действительно создают «чистые» пучки. Если, скажем, наш прибор Штерна—Герлаха недостаточно хорошо отделяет пучки друг от друга, то мы не можем произвести полного разделения на базисные состояния. Мы можем проверить, есть ли у нас чистые базисные состояния, посмотрев, смогут ли пучки опять расщепиться еще одним таким же фильтром. Если, например, имеется чистое состояние (+ T ), то все атомы пройдут через

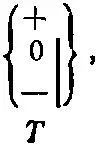
но ни один из них не пройдет ни через

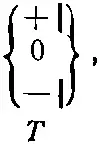
ни через

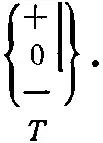
Наше утверждение относительно базисных состояний означает, что есть возможность отфильтровать пучок до некоторого чистого состояния, так что дальнейшее фильтрование идентичным прибором уже станет невозможным.

Следует еще отметить, что все, что мы говорим, до конца верно лишь в идеализированных случаях. В каждом реальном приборе Штерна—Герлаха надо подумать и о дифракции на щелях, которая может вынудить некоторые атомы перейти в состояния, отвечающие другим углам, и о том, нет ли в пучке атомов с другой степенью возбуждения своих внутренних состояний и т. д. Мы идеализировали наш случай и говорим только о тех состояниях, которые расщепляются в магнитном поле; при этом мы игнорируем все, что касается местоположения, импульса, внутренних возбуждений и т. п. Вообще же следовало бы рассматривать также базисные состояния, рассортированные и по отношению ко всем перечисленным характеристикам. Но для простоты мы пользуемся только нашей совокупностью трех состояний. Этого вполне достаточно для того, чтобы точно рассмотреть идеализированный случай, в котором атомы не подвергаются в приборе плохому обращению, не разрываются и, более того, покидая его, оказываются в состоянии покоя.

Заметьте, что мы всегда начинаем наши мысленные эксперименты с того, что берем фильтр, у которого открыт только один канал, так что начинаем всегда с определенного базисного состояния. Мы делаем это потому, что атомы выходят из печи в различных состояниях, случайно определенных тем, что произойдет в печи. (Это дает так называемый «неполяризованный» пучок.) Эта случайность предполагает вероятности «классического» толка (как при бросании монеты), которые отличаются от интересующих нас сейчас квантовомеханических вероятностей. Работа с неполяризованным пучком привела бы нас к добавочным усложнениям, а их лучше избегать, пока мы не поймем поведения поляризованных пучков. Так что пока не пытайтесь размышлять о том, что случится, если первый аппарат пропустит сквозь себя больше одного пучка. (В конце главы мы расскажем вам, как нужно поступать и в таких случаях.)