Ричард Фейнман - Том 3. Квантовая механика

Как обычно, это надо читать справа налево:

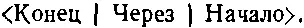
Если случайно окажется, это А ничего не меняет, а просто является открытым каналом, тогда мы пишем

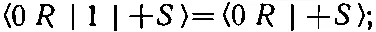(3.29)

эти два символа равнозначны. В более общих задачах мы можем заменить (+ S ) общим начальным состоянием φ, а (0 R ) — общим конечным состоянием χ и захотеть узнать амплитуду

Полный анализ прибора А должен был бы дать нам амплитуду <���χ| А |φ> для каждой мыслимой пары состояний φ и χ — бесконечное количество комбинаций! Как же сможем мы тогда дать краткое описание поведения прибора А ? Это можно сделать следующим путем. Вообразим, что мы видоизменили прибор (3.28) так:

(3.30)

На самом деле это вовсе не видоизменение, потому что широко раскрытые приборы Т ничего нигде не меняют. Но они подсказывают нам, как проанализировать проблему. Имеется определенная совокупность амплитуд < i |+ S > того, что атомы из S перейдут в состояние i прибора Т . Затем имеется другая совокупность амплитуд того, что состояние i (по отношению к Т ), войдя в А , выйдет оттуда в виде состояния j (по отношению к Т ). И наконец, имеется амплитуда того, что каждое состояние j пройдет через последний фильтр в виде состояния (0 R ). Для каждого допустимого пути существует амплитуда вида

и полная амплитуда есть сумма членов, которые можно получить из всех сочетаний i и j . Нужная нам амплитуда равна

(3.31)

Если (0R) и (+ S ) заменить общими состояниями χ и φ, то получится выражение такого же рода; так что общий результат выглядит так:

(3.32)

Теперь заметьте, что правая часть (3.32) на самом деле «проще» левой части. Прибор А полностью описан девятью числами < j | А | i >, сообщающими, каков отклик А на три базисных состояния прибора Т . Как только мы узнаем эту девятку чисел, мы сможем управиться с любой парой входных и выходных состояний φ и χ, если только определим каждое из них через три амплитуды перехода в каждое из трех базисных состояний (или выхода из них). Результат опыта предсказывается с помощью уравнения (3.32).

В этом и состоит основной вывод квантовой механики частицы со спином 1. Каждое состояние описывается тройкой чисел — амплитудами пребывания в каждом из базисных состояний (из избранной их совокупности). Всякий прибор описывается девяткой чисел — амплитудами перехода в приборе из одного базисного состояния в другое. Зная эти числа, можно подсчитать что угодно.

Девятка амплитуд, описывающая прибор, часто изображается в виде квадратной матрицы, именуемой матрицей < j | A | i >:

(3.33)

Вся математика квантовой механики является простым расширением этой идеи. Приведем несложный пример. Пусть имеется прибор С , который мы хотим проанализировать, т. е. рассчитать различные < j | С | i >. Скажем, мы хотим знать, что случится в эксперименте типа

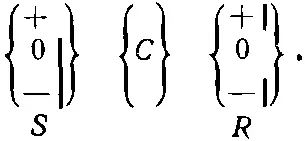(3.34)

Но затем мы замечаем, что С просто состоит из двух частей, стоящих друг за другом приборов А и В . Сперва частицы проходят через А , а потом — через B , т. е. можно символически записать

(3.35)

Мы можем прибор С назвать «произведением» А и В . Допустим также, что мы уже знаем, как эти две части анализировать; таким образом, мы можем узнать матрицы А и В (по отношению к Т ). Тогда наша задача решена. Мы легко найдем <���χ| С |φ> для любых входных и выходных состояний. Сперва мы напишем

Понимаете, почему? ( Подсказка : представьте, что между А и В поставлен прибор Т .) Если мы затем рассмотрим особый случай, когда φ и χ также базисные состояния (прибора Т ), скажем i и j , то получим

(3.36)

Это уравнение дает нам матрицу прибора «произведения» С через матрицы приборов А и В . Математики именуют новую матрицу < j | С | i >, образованную из двух матриц < j | В | i > и < j | А | i > в соответствии с правилом, указанным в (3.36), матричным «произведением» ВА двух матриц В и А . (Заметьте, что порядок существен, АВ ≠ ВА .) Итак, можно сказать, что матрица для стоящих друг за другом двух частей прибора — это матричное произведение матриц для этих двух приборов порознь (причем первый прибор стоит в произведении справа ). И каждый, кто знает матричную алгебру, поймет, что речь идет просто об уравнении (3.36).

Мы хотим сделать одно заключительное замечание относительно базисных состояний, используемых в расчетах. Предположим, мы захотели работать с каким-то определенным базисом, скажем с базисом S , а кто-то другой решает провести те же расчеты с другим базисом, скажем с базисом Т .

Для конкретности назовем наши базисные состояния состояниями ( iS ), где i =+, 0, -, а его базисные состояния назовем ( jT ). Как сравнить его работу с нашей? Окончательные ответы для результатов любых измерений обязаны оказаться одинаковыми, но употребляемые в самих расчетах всевозможные матрицы и амплитуды будут другими.