Ричард Фейнман - Том 3. Квантовая механика

Рассмотрим частный случай, когда φ 1=0, так что потенциальная энергия в первом ящике равна нулю, во втором же пусть q φ 2будет отрицательно, так что классически частица в нем будет обладать большей кинетической энергией. В классическом смысле она во втором ящике будет двигаться быстрее, у нее будет, стало быть, и больший импульс. Посмотрим, как это может получиться из квантовой механики.

При наших предположениях амплитуда в первом ящике должна была быть пропорциональна

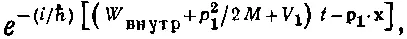(5.21)

а во втором

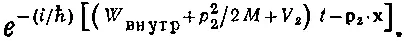(5.22)

(Будем считать, что внутренняя энергия не изменяется, а остается в обеих областях одной и той же.) Вопрос заключается в следующем: как эти две амплитуды сопрягаются друг с другом в области между ящиками?

Мы будем считать, что все потенциалы во времени постоянны, так что в условиях ничего не меняется. Затем мы предположим, что изменения амплитуды (т. е. ее фазы) всюду обладают одной и той же частотой , потому что в «среде» между ящиками нет, так сказать, ничего, что бы зависело от времени. Если в пространстве ничего не меняется, то можно считать, что волна в одной области «генерирует» во всем пространстве вспомогательные волны, которые все колеблются с одинаковой частотой и, подобно световым волнам, проходящим через покоящееся вещество, не меняют своей частоты. Если частоты в (5.21) и (5.22) одинаковы, то должно выполняться равенство

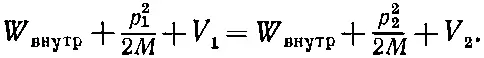(5.23)

Здесь по обе стороны стоят просто классические полные энергии, так что (5.23) есть утверждение о сохранении энергии. Иными словами, классическое утверждение о сохранении энергии вполне равноценно квантовомеханическому утверждению о том, что частоты у частицы всюду одинаковы, если условия во времени не меняются. Все это согласуется с представлением о том, что ℏ ω= E .

В том частном случае, когда V 1=0, а V 2отрицательно, (5.23) означает, что p 2больше р 1, т. е. в области 2 волны короче. Поверхности равной фазы показаны на фиг. 5.3 пунктиром. Там еще вычерчен график вещественной части амплитуды, из которого тоже видно, как уменьшается длина волны при переходе от области 1 в область 2. Групповая скорость волн, равная р / М , тоже возрастает так, как и следовало ожидать из классического сохранения энергии, потому что оно просто совпадает с (5.23).

Существует интересный частный случай, когда V 2становится столь большим, что V 2- V 1уже превышает p 2 1/2 M . Тогда p 2 2, даваемое формулой

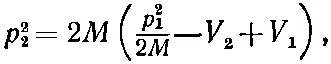(5.24)

становится отрицательным . А это значит, что р 2— мнимое число, скажем ip '. Классически мы бы сказали, что частица никогда не попадет в область 2, ей не хватит энергии, чтобы взобраться на потенциальный холм. Однако в квантовой механике амплитуда по-прежнему представляется уравнением (5.22); ее изменения в пространстве по-прежнему следуют закону

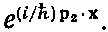
Но раз p 2— мнимое число, то пространственная зависимость превращается в вещественную экспоненту. Если, скажем, частица сперва двигалась в направлении + х , то амплитуда начнет меняться, как

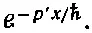(5.25)

С ростом х она быстро падает.

Вообразим, что обе области с разными потенциалами расположены очень тесно друг к другу, так что потенциальная энергия внезапно изменяется от V 1к V 2(фиг. 5.4, а).

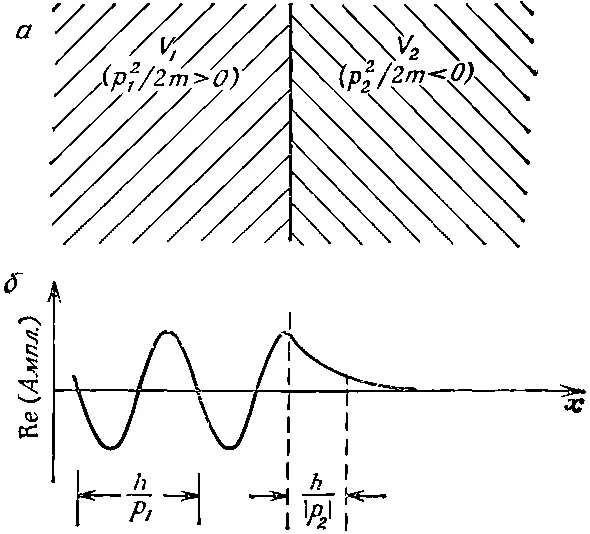
Фиг. 5.4. Амплитуда для частицы, приближающейся к сильно отталкивающему потенциалу.

Начертив график вещественной части амплитуды вероятности, мы получим зависимость, показанную на фиг. 5.4, б . Волна в области 1 отвечает частице, пытающейся попасть в область 2, но там амплитуда быстро спадает. Имеется какой-то шанс, что ее заметят в области 2, где классически она ни за что бы не оказалась, но амплитуда этого очень мала (кроме места близ самой границы). Положение вещей очень похоже на то, что мы обнаружили для полного внутреннего отражения света. Обычно свет не выходит, но его можно все же заметить, если поставить что-нибудь на расстоянии в одну-две длины волны от поверхности.

Вспомните, что если поместить вторую поверхность вплотную к границе, где свет полностью отражался, то можно добиться того, чтобы во втором куске вещества все же распространялся какой-то свет. То же самое происходит и с частицами в квантовой механике. Если имеется узкая область с таким высоким потенциалом V , что классическая кинетическая энергия там отрицательна, то частица никогда не пройдет сквозь нее. Но в квантовой механике экспоненциально убывающая амплитуда может пробиться сквозь эту область и дать слабую вероятность того, что частицу обнаружат по другую сторону — там, где кинетическая энергия опять положительна. Все это изображено на фиг. 5.5.

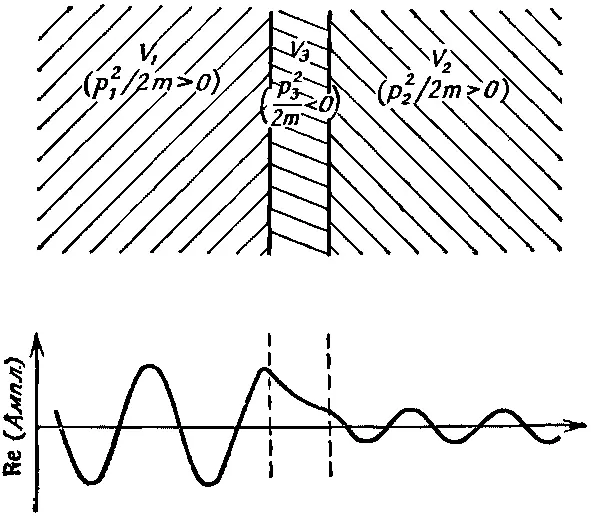
Фиг. 5.5. Проникновение амплитуды сквозь потенциальный барьер.

Эффект называется квантовомеханическим «проникновением сквозь барьер».

Проникновение квантовомеханической амплитуды сквозь барьер дает объяснение (или описание) α-распада ядра урана. Кривая зависимости потенциальной энергии α-частицы от расстояния от центра показана на фиг. 5.6, а .

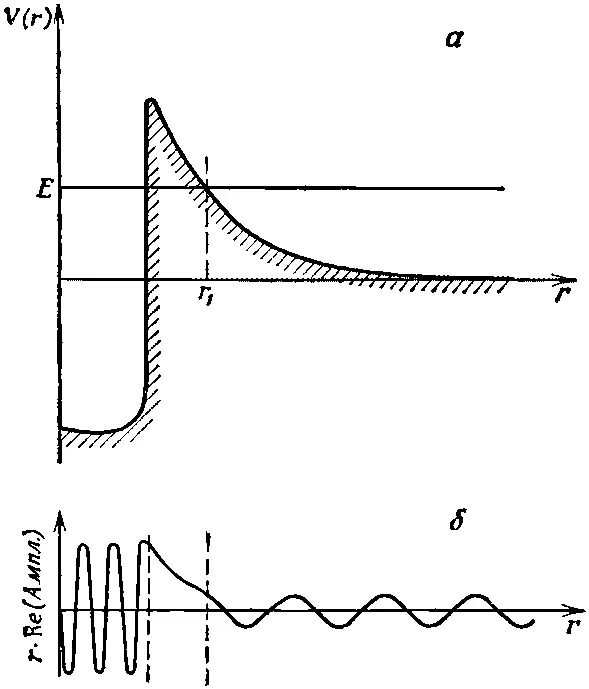
Фиг. 5.6. Потенциал α-частицы в ядре урана (а) и качественный вид амплитуды вероятности (б).

Если бы попытаться выстрелить α-частицей с энергией Е в ядро , то она почувствовала бы электростатическое отталкивание от ядерного заряда z и по классическим канонам не подошла бы к ядру ближе, чем на такое расстояние r 1при котором ее полная энергия сравняется с потенциальной V . Но где-то внутри ядра потенциальная энергия окажется намного ниже из-за сильного притяжения короткодействующих ядерных сил. Как же тогда объяснить, отчего при радиоактивном распаде мы обнаруживаем α-частицы, которые, первоначально находясь внутри ядра, оказываются затем снаружи него с энергией Е ? Потому что они с самого начала обладая энергией E , «просочились» сквозь потенциальный барьер. Схематичный набросок амплитуды вероятности дан на фиг. 5.6, б , хотя на самом деле экспоненциальный спад много сильнее, чем показано. Весьма примечательно, что среднее время жизни α-частицы в ядре урана достигает 4 1/ 2миллиарда лет, тогда как естественные колебания внутри ядра чрезвычайно быстры, их в секунду бывает 10 22! Как же можно из 10 -22 сек получить число порядка 10 9лет? Ответ состоит в том, что экспонента дает неслыханно малый множитель порядка 10 -45, что и приводит к очень малой, хоть и вполне определенной, вероятности просачивания. Если уж α-частица попала в ядро, то почти нет никакой амплитуды обнаружить ее не в ядре; если, однако, взять таких ядер побольше и подождать подольше, то вам, может быть, повезет и вы увидите, как частица выскочит наружу.