Ричард Фейнман - Том 3. Квантовая механика

Тем же методом, конечно, можно воспользоваться, чтобы ответить на другие вопросы, касающиеся распада мюона. Например, как зависит от времени t шанс заметить распадный электрон в направлении у , под 90° к направлению х , но по-прежнему под прямым углом к полю? Если вы решите эту задачу, то увидите, что вероятность оказаться в состоянии (+ у ) меняется как cos 2{(μ Bt / ℏ )-(π/4)}; она колеблется с тем же периодом, но достигает максимума на четверть цикла позже, когда μВt/ℏ=π/4. На самом-то деле происходит вот что: с течением времени мюон проходит через последовательность состояний, отвечающих полной поляризации в направлении, которое непрерывно вращается вокруг оси z . Это можно описать, говоря, что спин прецессирует с частотой

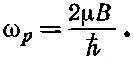(5.38)

Вам должно становиться понятно, в какую форму выливается квантовомеханическое описание, когда мы описываем поведение чего-либо во времени.

Повторить : гл. 49) (вып. 4) «Собственные колебания»

Прежде чем приступить к основной теме этой главы, мы хотели бы изложить несколько математических идей, которые часто встречаются в книгах по квантовой механике. Знание их облегчит вам чтение других книг или статей по этому предмету. Первая идея — это тесное математическое подобие между уравнениями квантовой механики и формулами для скалярного произведения двух векторов. Вы помните, что если χ и φ — два состояния, то амплитуда начать в φ и кончить в χ может быть записана в виде суммы (по полной совокупности базисных состояний) амплитуд перехода из φ в одно из базисных состояний и затем из этого базисного состояния уже в χ:

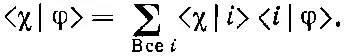(6.1)

Мы объясняли это при помощи прибора Штерна—Герлаха, но сейчас напоминаем вам, что в этих приборах нет нужды. Уравнение (6.1) — это математический закон, который верен всегда, все равно, есть ли у нас фильтровальное оборудование или нет; вообще совсем не обязательно воображать наличие какого-то прибора. Можно рассматривать это просто как формулу для амплитуды <���χ|φ>.

Сопоставим (6.1) с формулой для скалярного произведения двух векторов Ви А. Если Ви А— обычные трехмерные векторы, то скалярное произведение можно написать так:

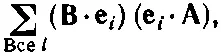
считая, что символ е iобозначает любой из трех единичных векторов в направлениях х, у и z. Тогда B·e 1 — это то, что обычно называют В х , а В·е 2 — то, что обычно называют B y , и т. д. Значит, (6.2) эквивалентно

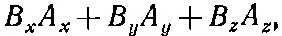
а это и есть скалярное произведение В·А.

Сравнение (6.1) с (6.2) обнаруживает следующую аналогию. Состояния χ и φ соответствуют двум векторам Аи В. Базисные состояния i отвечают специальным векторам е i, к которым мы относим все прочие векторы. Любой вектор может быть представлен как линейная комбинация трех «базисных векторов» е i. Далее, если вам известны коэффициенты при каждом «базисном векторе» в этой комбинации, т. е. три его компоненты, то вы знаете о векторе все. Точно так же любое квантовомеханическое состояние может быть полностью описано амплитудами < i |φ> перехода в базисные состояния, и если эти коэффициенты вам известны, то вы знаете все, что можно знать о состоянии. Из-за этой тесной аналогии то, что мы назвали «состоянием», часто именуют «вектором состояния».

Раз базисные векторы е i перпендикулярны друг другу, то существует соотношение

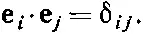(6.3)

Это соответствует соотношению (3.25) между базисными состояниями i

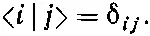(6.4)

Теперь вы понимаете, почему говорят, что базисные состояния i все «ортогональны друг другу».

Между (6.1) и скалярным произведением есть одно минимальное различие. У нас

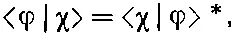(6.5)

а в векторной алгебре

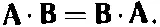
В квантовой механике с ее комплексными числами мы обязаны выдерживать порядок множителей, а в скалярном произведении порядок неважен.

Теперь рассмотрим такое векторное уравнение:

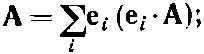(6.6)

оно немножко необычно, но тем не менее верно. И означает оно то же самое, что и

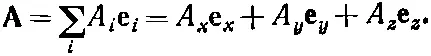(6.7)

Заметьте, однако, что в (6.6) входит величина, отличная от скалярного произведения. Скалярное произведение — это просто число , а (6.6) — векторное уравнение. Одним из великих приемов векторного анализа было абстрагировать от уравнений идею самого вектора . Равным образом можно попытаться абстрагировать от уравнения (6.1) то, что в квантовой механике является аналогом «вектора». И это действительно можно сделать. Уберем <���χ| по обе стороны (6.1) и напишем такое уравнение (не пугайтесь — это просто обозначение, и через пару минут вы узнаете, что означают эти символы):

(6.8)

Скобку <���χ|φ> представляют себе состоящей из двух половинок. Вторую половинку |φ> называют кет, а первую <���χ| называют брэ (поставленные рядом они образуют брэ-кет≡bгаcket, скоб-ка≡скобка — обозначение, предложенное Дираком); полусимволы <���χ| и |φ> также называют векторами состояний . Это не числа отнюдь, а нам вообще-то нужно, чтобы результаты наших расчетов выражались числами; стало быть, такие «незаконченные» величины представляют собой промежуточные шаги в расчетах.

До сих пор мы все свои результаты выражали с помощью чисел. Как же мы умудрялись избегать векторов? Забавно, что даже в обычной векторной алгебре можно сделать так, чтобы во все уравнения входили только числа. Например, вместо векторного уравнения типа