Ричард Фейнман - Том 3. Квантовая механика

Предположим, что частица движется сквозь область, где есть потенциал, меняющийся поперек движения. Классически мы бы описали этот случай так, как показано на фиг. 5.7.

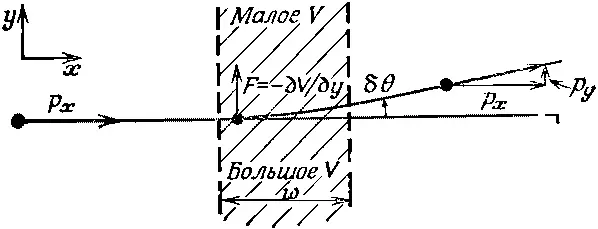
Фиг. 5.7. Отклонение частицы поперечным градиентом потенциала.

Если частица движется в направлении х и вступает в область, где имеется потенциал, изменяющийся вдоль y , то частица получит поперечное ускорение от силы F =-∂ V /∂ y . Если сила присутствует только в ограниченной области шириной w , то она будет действовать только в течение времени w / v . Частица получит поперечный импульс

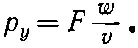
Тогда угол отклонения δθ будет равен

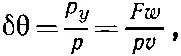
где р — начальный импульс. Подставляя вместо F число -∂ V /∂ y , получаем

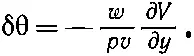(5.26)

Теперь нам предстоит выяснить, удастся ли получить этот результат с помощью представления о том, что волны подчиняются уравнению (5.20). Мы рассмотрим то же самое явление квантовомеханически, предполагая, что все масштабы в нем намного превосходят длины волн наших амплитуд вероятности. В любой маленькой области можно считать, что амплитуда меняется как

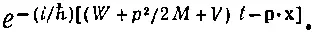(5.27)

В состоянии ли мы увидеть, как отсюда получится отклонение частиц, когда у V будет поперечный градиент? На фиг. 5.8 мы прикинули, как будут выглядеть волны амплитуды вероятности.

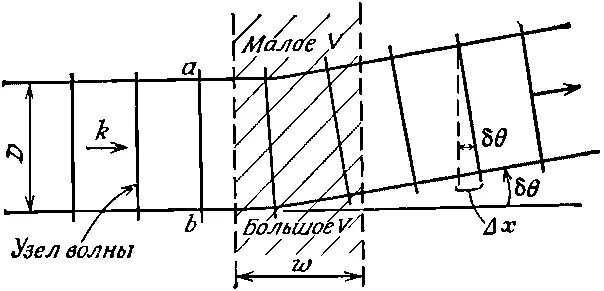
Фиг. 5.8. Амплитуда вероятности в области с поперечным градиентом потенциала.

Мы начертили ряд «узлов волн», которые вы можете считать, скажем, поверхностями, где фаза амплитуды равна нулю. В любой небольшой области длина волны (расстояние между соседними узлами) равна

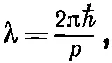
где р связано с V формулой

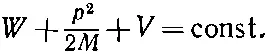(5.28)

В области, где V больше, там р меньше, а волны длиннее. Поэтому направление линий узлов волн постепенно меняется, как показано на рисунке.

Чтобы найти изменение наклона линий узлов волн, заметим, что на двух путях а и b имеется разность потенциалов Δ V =(∂ V /∂ y ) D , а значит, и разница Δ р между импульсами. Эту разность можно получить из (5.28):

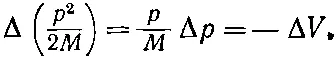(5.29)

Волновое число p / ℏ поэтому тоже на разных путях различно, что означает, что фазы растут вдоль них с разной скоростью. Разница в скорости роста фазы есть Δ k =Δ р /ℏ, и накопленная на всем пути w разность фаз будет равна

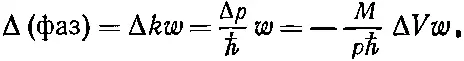(5.30)

Это число показывает, на сколько к моменту выхода из полосы фаза вдоль пути b «опережает» фазу вдоль пути а . Но на выходе из полосы такое опережение фаз отвечает опережению узла волны на величину

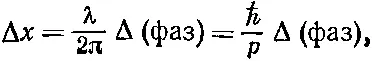
или

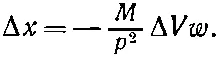(5.31)

Обращаясь к фиг. 5.8, мы видим, что новый фронт волны повернется на угол δθ, даваемый формулой

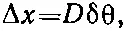(5.32)

так что мы имеем

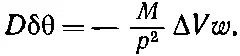(5.33)

А это совпадает с (5.26), если заменить р / М на v , а Δ V / D на ∂ V /∂ y .

Результат, который мы только что получили, верен лишь, когда потенциал меняется медленно и плавно — в так называемом классическом пределе . Мы показали, что при этих условиях получим те же движения частиц, что получились бы и из F= m a, если предположить, что потенциал дает вклад в фазу амплитуды вероятности, равный Vt / ℏ. В классическом пределе квантовая механика оказывается в согласии с ньютоновской механикой .

Заметьте, что мы не предполагали, что потенциальная энергия у нас какая-то особая, это просто энергия, производная от которой дает силу. Например, в опыте Штерна—Герлаха энергия имела вид U =- μ·B; отсюда при наличии у Впространственной вариации и получалась сила. Если бы нам нужно было квантовомеханическое описание опыта, мы должны были бы сказать, что у частиц в одном пучке энергия меняется в одну сторону, а в другом пучке — в обратную сторону. (Магнитную энергию U можно было бы вставить либо в потенциальную энергию V , либо во «внутреннюю» энергию W ; куда именно, совершенно неважно.) Из-за вариаций энергии волны преломляются, пучки искривляются вверх или вниз. (Мы теперь знаем, что квантовая механика предсказывает то же самое искривление, которое следует и из расчета по классической механике.)

Из зависимости амплитуды от потенциальной энергии также следует, что у частицы, сидящей в однородном магнитном поле, направленном по оси z, амплитуда вероятности обязана меняться во времени по закону

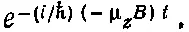
(Можно считать это просто определением μ z.) Иначе говоря, если поместить частицу в однородное поле В на время τ, то ее амплитуда вероятности умножится на

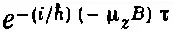
сверх того, что было бы без поля. Поскольку у частицы со спином 1/ 2величина μ zможет быть равна плюс или минус какому-то числу, скажем μ, то у двух мыслимых состояний в однородном поле фазы будут меняться с одинаковой скоростью в противоположные стороны. Амплитуды помножатся на