Ричард Фейнман - Том 3. Квантовая механика

А общее решение для электронов у нас есть! Пусть вначале электрон обладает определенным состоянием, в котором спин направлен вверх по некоторому направлению, а магнитное поле В— в какую-то другую сторону. Вращайте просто направление спина вокруг оси Вс векторной угловой скоростью ω( t ), равной некоторой константе, умноженной на вектор В(а именно ω=2μ В/ ℏ ). Если Вменяется со временем, двигайте по-прежнему ось вращения так, чтобы она оставалась параллельной В, и изменяйте скорость вращения так, чтобы она все время была пропорциональна напряженности В(фиг. 8.11).

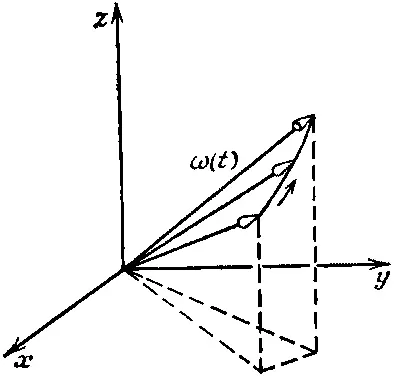
Фиг. 8.11. Направление спина электрона в изменяющемся магнитном поле В(t) прецессирует с частomoй ω(t) вокруг оси, параллельной В.

Если все время это делать, вы остановитесь на какой-то конечной ориентации спиновой оси, и амплитуды С 1и С 2получатся просто как ее проекции [при помощи (8.30)] на вашу систему координат.

Вы видите, что задача эта чисто геометрическая: надо заметить, где закончились все ваши вращения. Хотя сразу видно, что для этого требуется, но эту геометрическую задачу (отыскание окончательного итога вращений с переменным вектором угловой скорости) нелегко в общем случае решить явно. Во всяком случае, мы в принципе видим общее решение любой задачи для двух состояний. В следующей главе мы глубже исследуем математическую технику обращения с частицами спина 1/ 2и, следовательно, обращения с системами, обладающими двумя состояниями, в общем случае.

Повторить : гл. 33 (вып. 3) «Поляризация»

Продолжаем обсуждение свойств двухуровневых систем. В конце предыдущей главы мы говорили о частице со спином 1/ 2в магнитном поле. Мы описывали спиновое состояние, задавая амплитуду С 1того, что z-компонента спинового момента количества движения равна + ℏ /2, и амплитуду С 2того, что она равна - ℏ /2. В предыдущих главах мы эти базисные состояния обозначали |+> и |->. Прибегнем опять к этим обозначениям, хотя, когда это будет удобнее, мы будем менять их на |1> и |2>.

Мы видели в последней главе, что когда частица со спином 1/ 2и с магнитным моментом μ находится в магнитном поле В=( В x , В y , B z ), то амплитуды С +(= C 1) и С -(= С 2) связаны следующими дифференциальными уравнениями:

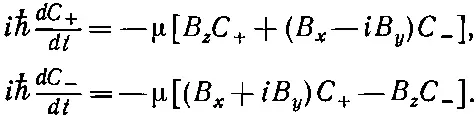(9.1)

Иначе говоря, матрица-гамильтониан H ij имеет вид

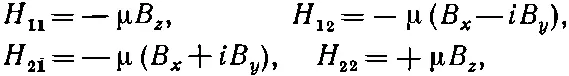(9.2)

конечно, уравнения (9.1) совпадают с

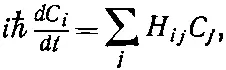(9.3)

где i и j принимают значения + и - (или 1 и 2).

Эта система с двумя состояниями — спин электрона — настолько важна, что очень полезно было бы найти для ее описания способ поаккуратнее и поизящнее. Мы сейчас сделаем небольшое математическое отступление, чтобы показать вам, как обычно пишутся уравнения системы с двумя состояниями. Это делается так: во-первых, заметьте, что каждый член гамильтониана пропорционален μ и некоторой компоненте В; поэтому ( чисто формально ) можно написать

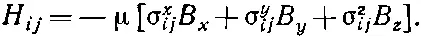
Здесь нет какой-либо новой физики; эти уравнения просто означают, что коэффициенты σ x ij, σ y ij, и σ z ij— их всего 4×3=12 — могут быть представлены так, что (9.4) совпадет с (9.2).

Посмотрим, почему это так. Начнем с B z. Раз В zвстречается только в H 11и H 22, то все будет в порядке, если взять

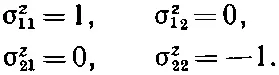
Мы часто пишем матрицу H ij в виде таблички такого рода:

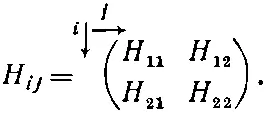
Для гамильтониана частицы со спином 1/ 2в магнитном поле В—это все равно что

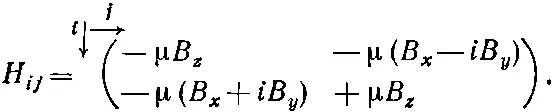
Точно так же и коэффициенты σ z ijможно записать в виде матрицы

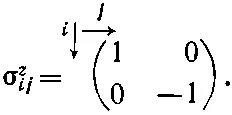(9.5)

Расписывая коэффициенты при В х , получаем, что элементы матрицы σ х должны иметь вид

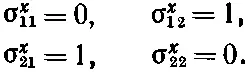
Или сокращенно:

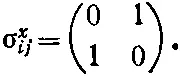(9.6)

И наконец, глядя на B y , получаем

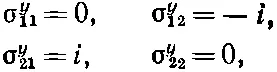
или

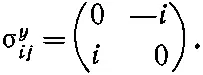(9.7)

Если так определить три матрицы сигма, то уравнения (9.1) и (9.4) совпадут. Чтоб оставить место для индексов i и j , мы отметили, какая σ стоит при какой компоненте В, поставив индексы х, у, z сверху. Обычно, однако, i и j отбрасывают (их легко себе и так вообразить), а индексы х, у и z ставят внизу. Тогда (9.4) записывается так:

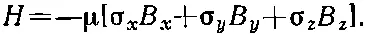(9.8)

Матрицы сигма так важны (ими беспрерывно пользуются), что мы выписали их в табл. 9.1. (Тот, кто собирается работать в квантовой физике, обязан запомнить их.) Их еще называют спиновыми матрицами Паули — по имени физика, который их выдумал.

Таблица 9.1. СПИНОВЫЕ МАТРИЦЫ ПАУЛИ

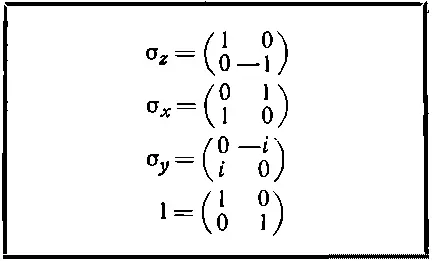
В таблицу мы включили еще одну матрицу 2×2, которая бывает нужна тогда, когда мы хотим рассматривать систему, оба спиновых состояния которой имеют одинаковую энергию, или когда хотим перейти к другой нулевой энергии. В таких случаях к первому уравнению в (9.1) приходится добавлять E 0 С +, а ко второму Е 0 С -. Это можно учесть, введя новое обозначение — единичную матрицу «1», или δ ij: