Ричард Фейнман - Том 3. Квантовая механика

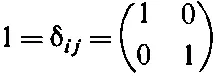(9.9)

переписав (9.8) в виде

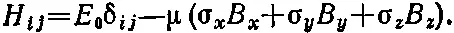(9.10)

Обычно просто понимают без лишних оговорок , что любая константа наподобие Е 0автоматически умножается на единичную матрицу, и тогда пишут просто

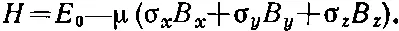(9.11)

Одна из причин, отчего спиновые матрицы так полезны, — это что любая матрица 2×2 может быть выражена через них. Во всякой матрице стоят четыре числа, скажем

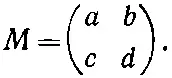
Ее всегда можно записать в виде линейной комбинации четырех матриц. Например,

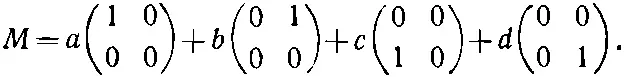
Это можно делать по-всякому, но, в частности, можно сказать, что М состоит из какого-то количества σ x плюс какое-то количество σ y и т. д., и написать

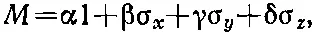
где «количества» α, β, γ и δ в общем случае могут быть комплексными числами.

Раз любая матрица 2×2 может быть выражена через единичную матрицу и матрицу сигма, то все, что может понадобиться для любой системы с двумя состояниями, у нас уже есть. Какой бы ни была система с двумя состояниями — молекула аммиака, краситель фуксин, что угодно, — гамильтоново уравнение может быть переписано в сигмах. Хотя в физическом случае электрона в магнитном поле сигмы кажутся имеющими геометрический смысл, но их можно считать и просто полезными матрицами, пригодными к употреблению во всякой системе с двумя состояниями.

Например, один из способов рассмотрения протона и нейтрона — это представлять их как одну и ту же частицу в любом из двух состояний. Мы говорим, что нуклон (протон или нейтрон) есть система с двумя состояниями, в данном случае состояниями по отношению к электрическому заряду. Если рассматривать нуклон таким образом, то состояние |1> может представлять протон, а |2> — нейтрон. Говорят, что у нуклона есть два состояния «изотопспина».

Поскольку мы будем применять матрицы сигма в качестве «арифметики» квантовой механики систем с двумя состояниями, то наскоро познакомимся с соглашениями матричной алгебры. Под «суммой» двух или большего числа матриц подразумевается как раз то, что имелось в виду в уравнении (9.4).

Вообще если мы «складываем» две матрицы А и В , то «сумма» С означает, что каждый ее элемент C ij дается формулой

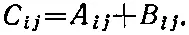
Каждый элемент С есть сумма элементов А и В , стоящих на тех же самых местах.

В гл. 3, § 6, мы уже сталкивались с представлением о матричном «произведении». Та же идея полезна и при обращении с матрицами сигма. В общем случае «произведение» двух матриц A и В (в этом именно порядке) определяется как матрица С с элементами

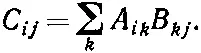(9.12)

Это — сумма произведений элементов, взятых попарно из i -й строчки А и k -го столбца В . Если матрицы расписаны в виде таблиц, как на фиг. 9.1, то можно указать удобную «систему» получения элементов матрицы-произведения.

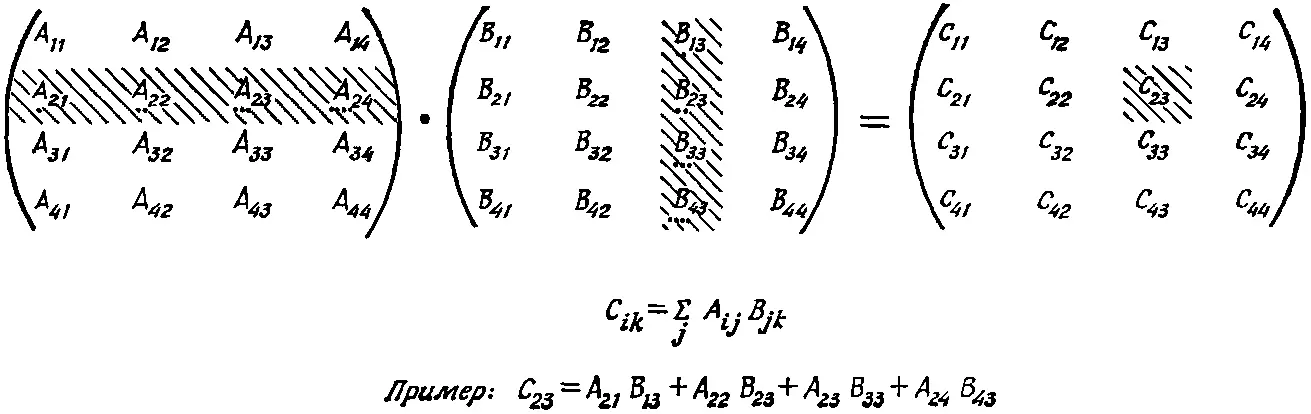
Фиг. 9.1. Перемножение двух матриц.

Скажем, вы вычисляете С 23. Вы двигаете левым указательным пальцем по второй строчке А , а правым — вниз по третьему столбцу В , перемножаете каждую пару чисел и складываете пары по мере движения. Мы попытались изобразить это на рисунке.

Для матриц 2×2 это выглядит особенно просто. Например, если σ х умножается на σ x , то выходит

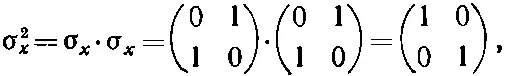
т. е. просто единичная матрица. Или, для примера, подсчитаем еще

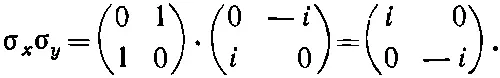
Взглянув на табл. 9.1, вы видите, что это просто матрица σ x , умноженная на i . (Вспомните, что умножение матрицы на число означает умножение каждого элемента матрицы на число.) Попарные произведения сигм очень важны и выглядят они довольно забавно, так что мы их выписали в табл. 9.2. Вы сами можете подсчитать их, как мы сделали это с σ х 2и σ х σ y .

Таблица 9.2. ПРОИЗВЕДЕНИЯ СПИНОВЫХ МАТРИЦ

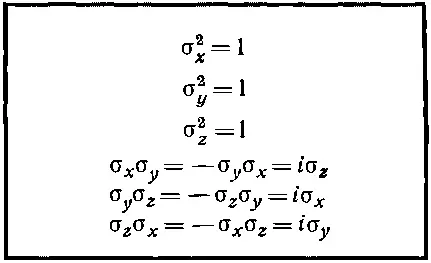
С матрицами σ связан еще один очень интересный и важный момент. Можно, если угодно, представить себе, что три матрицы σ х , σ y и σ z подобны трем компонентам вектора; его иногда именуют «вектором сигма» и обозначают σ. Это на самом деле «матричный вектор», или «векторная матрица». Это три разные матрицы, связанные каждая со своей осью х, у или z . С их помощью гамильтониан системы можно записать в красивом виде, пригодном для любой системы координат:

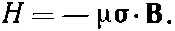(9.13)

Хотя мы записали эти три матрицы в представлении, в котором понятия «вверх» и «вниз» относятся к направлению z (так что σ zвыглядит особенно просто), но можно представить себе, как будут они выглядеть в любом другом представлении. И хотя это требует немалых выкладок, можно все же показать, что они изменяются как компоненты вектора. (Мы, впрочем, пока не будем заботиться о том, чтобы доказать это. Проверьте сами, если хотите.) Вы можете пользоваться σ в различных системах координат, как если бы это был вектор.

Вы помните, что гамильтониан Н связан в квантовой механике с энергией. Он действительно в точности совпадает с энергией в том простом случае, когда состояний только одно. Даже в системе с двумя состояниями, какой является спин электрона, если записать гамильтониан в виде (9.13), он очень напоминает классическую формулу энергии магнита с магнитным моментом μв магнитном поле В. Классически это выглядит так: