Ричард Фейнман - Том 3. Квантовая механика

Если хотите, идею «абстрагирования» можно продвинуть еще на шаг. Уравнение (9.19) справедливо для всякого состояния |ψ>. Кроме того, левая сторона iℏd / dt — это тоже оператор; его действие: «продифференцируй по t и умножь на iℏ ». Итак, (9.19) можно рассматривать как уравнение между операторами — операторное уравнение

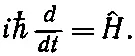
Оператор Гамильтона (с точностью до константы), действуя на любое состояние, приводит к тому же результату, что и d / dt . Помните, что это уравнение, как и (9.19), не есть утверждение о том, что оператор ^ H просто та же операция , что и d / dt . Эти уравнения — динамический закон природы (закон движения) для квантовой системы.

Только для того, чтобы попрактиковаться в этих представлениях, продемонстрируем вам другой вывод уравнения (9.18). Вы знаете, что любое состояние |ψ> можно записать через его проекции на какой-то базис [см. (6.8)]:

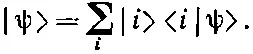(9.20)

Как же меняется |ψ> во времени? Продифференцируем его:

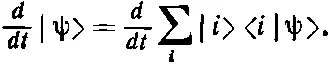(9.21)

Но базисные состояния | i > во времени не меняются (по крайней мере у нас они всегда были определенными, закрепленными состояниями), и только амплитуды < i |ψ> — это числа, которые могут меняться. Иначе говоря, (9.21) превращается в

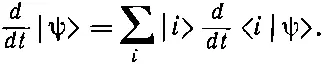(9.22)

Но ведь d < i |ψ>/dt нам известно—это (9.16); получается, следовательно,

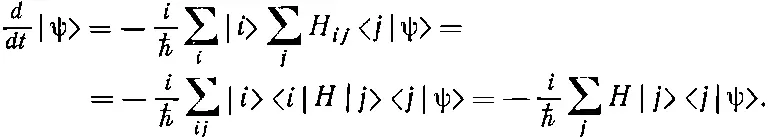
А это опять-таки уравнение (9.18).

Итак, на гамильтониан можно смотреть по-разному. Можно рассматривать совокупность коэффициентов H ij просто как компанию чисел, можно говорить об «амплитудах» < i | Н |j>, можно представлять себе «матрицу» H ij и можно считать его «оператором» ^ H . Все это одно и то же.

Вернемся теперь к нашей системе с двумя состояниями. Если уж мы записываем гамильтониан через матрицы сигма (с подходящими численными множителями, такими, как В х и т. д.), то естественно рассматривать и σ x ijкак амплитуду < i |σ х | j >, или, для краткости, как оператор ^σ x. Если применить эту идею оператора, то уравнение движения состояния |ψ> в магнитном поле можно написать в виде

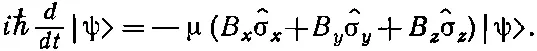(9.23)

Желая «использовать» это уравнение, нам, естественно, приходится выражать |ψ> через базисные векторы (равносильно тому, что приходится находить компоненты пространственных векторов, когда задача доводится до числа). Так что обычно мы предпочитаем расписывать (9.23) в более раскрытом виде:

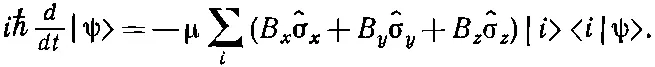(9.24)

Сейчас вы увидите, чем красива идея оператора. Чтобы применять уравнение (9.24), нужно знать, что будет, когда операторы ^ σподействуют на каждое базисное состояние. Напишем ^σ z |+>; это какой-то вектор |?>, но какой? Что ж, умножим его слева на <+| и получим

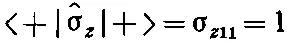
(пользуясь табл. 9.1). Итак, мы знаем, что

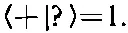(9.25)

Теперь умножим ^σ z|+> слева на <-|. Получится

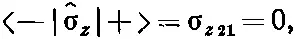
т, е.

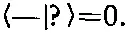(9.26)

Существует только один вектор состояния, удовлетворяющий и (9.25), и (9.26); это |+>. Мы, стало быть, открыли, что

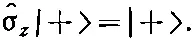(9.27)

Такого рода рассуждениями можно легко показать, что все свойства матриц сигма могут быть в операторных обозначениях описаны рядом правил, приведенных в табл. 9.3.

Таблица 9.3. СВОЙСТВА ОПЕРАТОРА ^σ

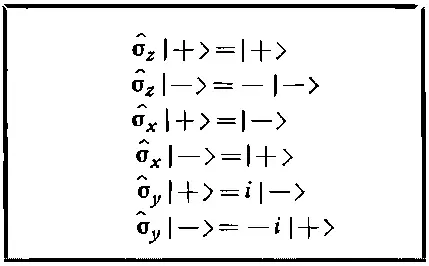
Если у нас есть произведения матриц сигма, то они переходят в произведения операторов. Когда два оператора стоят рядом в виде произведения, то сперва приступает к операции тот оператор, который стоит правее. Скажем, под ^σ x ^σ y |+> надо понимать ^σ х (^σ y |+>). Из табл. 9.3 получаем ^σ y |+>= i |-> так что

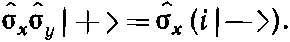(9.28)

Числа (как, например, i ) просто проходят сквозь операторы (операторы действуют только на векторы состояний); значит (9.28) перейдет в

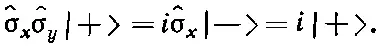
Если сделать то же самое с ^σ x ^σ y |->, то получится

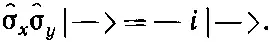
Если взглянуть на табл. 9.3, то видно, что ^σ х ^σ у , действуя на |+> или |->, даст в точности то же, что получается, если просто подействовать оператором ^σ z и умножить на — i . Поэтому можно сказать, что операция ^σ х ^σ y совпадает с операцией i ^σ z , и записать это утверждение в виде операторного уравнения

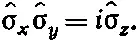(9.29)

Убедитесь, что это уравнение совпадает с одним из наших матричных уравнений табл. 9.2. Итак, мы опять видим соответствие между матричной и операторной точкой зрения. Каждое из уравнений в табл. 9.2 может поэтому рассматриваться и как уравнение относительно операторов сигма. Можно проверить, что они действительно следуют из табл. 9.3. Работая с этими вещами, лучше не следить за тем, являются ли величины типа σ или Н операторами или матрицами. Чем их ни считай, уравнения выйдут одни и те же, так что табл. 9.2 можно при желании относить то к операторам сигма, то к матрицам сигма.

Теперь можно писать наше уравнение двух состояний в различных видах, например: