Ричард Фейнман - Том 3. Квантовая механика

К примеру, если у нас есть поляроид, ось которого расположена так, чтобы пропускать свет, поляризованный в направлении, которое мы называем направлением х , и если мы направили туда фотон, который, как нам известно, находится в состоянии | у >, то он поглотится поляроидом. Если послать туда фотон, который, как нам известно, находится в состоянии | х >, он и выйдет в состоянии | x >. Когда мы берем кусок кальцита (исландского шпата), который расщепляет пучок поляризованного света на | x >-пучок и | y >-пучок, то этот кусок кальцита полностью аналогичен прибору Штерна—Герлаха, расщепляющему пучок атомов серебра на два состояния |+> и |->. Значит, все, что мы раньше делали с частицами и приборами Штерна—Герлаха, можно повторить со светом и кусками поляроида. А что можно сказать о свете, который отфильтрован куском поляроида, повернутым на угол θ? Другое ли это состояние? Да, действительно, это другое состояние. Обозначим ось поляроида х ', чтобы отличать ее от осей наших базисных состояний (фиг. 9.2).

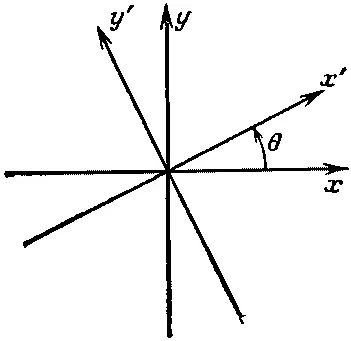
Фиг. 9.2. Оси координат, перпендикулярные к вектору импульса фотона.

Выходящий наружу фотон будет в состоянии | х '>. Но всякое состояние может быть представлено в виде линейной комбинации базисных состояний, а формула для такой комбинации известна:

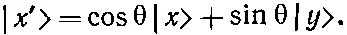(9.33)

Иначе говоря, если фотон пройдет сквозь кусок поляроида, повернутого на угол θ (по отношению к х ), он все равно может быть разрешен на | x >- и | y >-пучки (например, куском кальцита). Или, если угодно, вы можете в своем воображении просто разбить его на х - и y -компоненты. Любым путем вы получите амплитуду cosθ быть в | х >-состоянии и амплитуду sinθ быть в | y >-состоянии.

Теперь поставим такой вопрос: пусть фотон поляризован в направлении х ' куском поляроида, повернутого на угол θ, и пусть он попадет в другой поляроид, повернутый на угол нуль (фиг. 9.3).

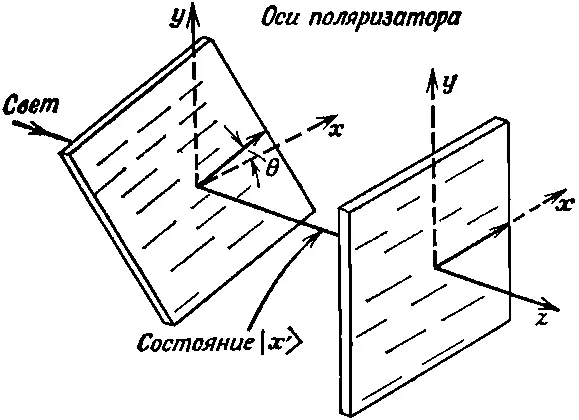
Фиг. 9.3. Две поляроидные пластины с углом θ между плоскостями поляризации.

Что тогда произойдет? С какой вероятностью он пройдет сквозь поляроид? Ответ : Пройдя первый поляроид, фотон наверняка оказывается в состоянии | х '>. Через второй поляроид он протиснется лишь в том случае, если будет в состоянии | x > (и поглотится им, оказавшись в состоянии | у >). Значит, мы спрашиваем, с какой вероятностью фотон окажется в состоянии | x >? Эту вероятность мы получим из квадрата модуля амплитуды , амплитуды того, что фотон в состоянии | х '> находится также и в состоянии | x >. Чему равно < x | x '>? Умножив (9.33) на < x |, получим

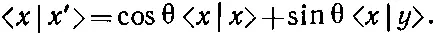
Но < x | y >=0; это следует из физики, так должно быть, если | х > и | у > суть базисные состояния, а < x | x >=1. И мы получаем

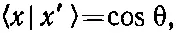
а вероятность равна cos 2θ. Например, если первый поляроид поставлен под углом 30°, то 3/ 4времени фотон будет проходить через него, а 1/ 4времени будет нагревать поляроид, поглощаясь внутри него.

Посмотрим теперь, что в такой же ситуации происходит с точки зрения классической физики. Там мы имели бы пучок света, электрическое поле которого меняется тем или иным образом, — скажем «неполяризованный» пучок. После того как он прошел бы через первый поляроид, электрическое поле величины ℰ начало бы колебаться в направлении х ' ; мы бы начертили его в виде колеблющегося вектора с пиковым значением ℰ 0на диаграмме фиг. 9.4.

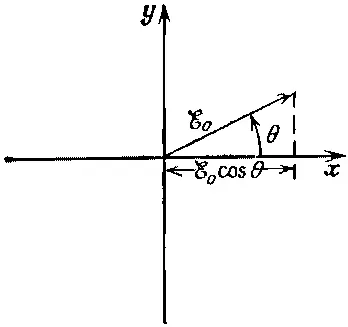
Фиг. 9.4. Классическая картина электрического вектора ℰ.

Если бы затем свет достиг второго поляроида, то через него прошла бы только x -компонента ℰ 0cosθ электрического поля. Интенсивность была бы пропорциональна квадрату поля, т. е. ℰ 0 2cos 2θ. Значит, проходящая сквозь последний поляроид энергия была бы в cos 2θ слабее энергии, поступающей в него.

И классическая, и квантовая картины приводят к одинаковым результатам. Если бы вы бросили на второй поляроид 10 миллиардов фотонов, а средняя вероятность прохождения каждого из них была бы, скажем, 3/ 4, то следовало бы ожидать, что сквозь него пройдет 3/ 4от 10 миллиардов. Равным образом и энергия, которую они унесли бы, составила бы 3/ 4той энергии, которую вам хотелось протолкнуть через поляроид. Классическая теория ничего не говорит о статистике этих вещей, она попросту утверждает, что энергия, которая пройдет насквозь, в точности равна 3/ 4той энергии, которая была пущена в поляроид. Это, конечно, немыслимо, если фотон только один. Не бывает 3/ 4фотона. Либо он весь здесь, либо его вовсе нет. И квантовая механика говорит нам, что он бывает весь здесь 3/ 4 времени . Связь обеих теорий ясна.

А как же с другими сортами поляризации? Скажем, с правой круговой поляризацией? В классической теории компоненты х и у правой круговой поляризации были равны, но сдвинуты по фазе на 90°. В квантовой теории фотон, поляризованный по кругу вправо («правый»), обладает равными амплитудами быть | х >- и | у >-поляризованным, и эти амплитуды сдвинуты по фазе на 90°. Обозначая состояние «правого» фотона через |П>, а состояние «левого» фотона через |Л>, можно написать [см. гл. 33, § 1 (вып. 3)]

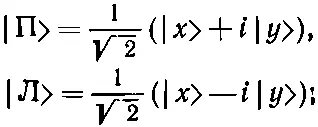(9.34)

множитель 1/√2 поставлен, чтобы нормировать состояния. С помощью этих состояний можно подсчитывать любые эффекты, связанные с фильтрами или интерференцией, применяя законы квантовой теории. При желании можно также выбрать в качестве базисных состояний |П> и |Л> и все представлять через них. Надо только предварительно убедиться, что <���П|Л>=0, а это можно сделать, взяв сопряженный вид первого уравнения [см. (6.13)] и перемножив их друг с другом. Можно раскладывать свет, пользуясь в качестве базиса и х -, и y -поляризациями, и х '-, и y '-поляризациями, а можно—и правой, и левой поляризациями.