Ричард Фейнман - Том 3. Квантовая механика

Но вы можете представить, куда он направился, применяя сохранение импульса и энергии. (Он затем иногда раскрывает свое местоположение, распадаясь на пару заряженных частиц, как показано на фиг. 9.5, а.)

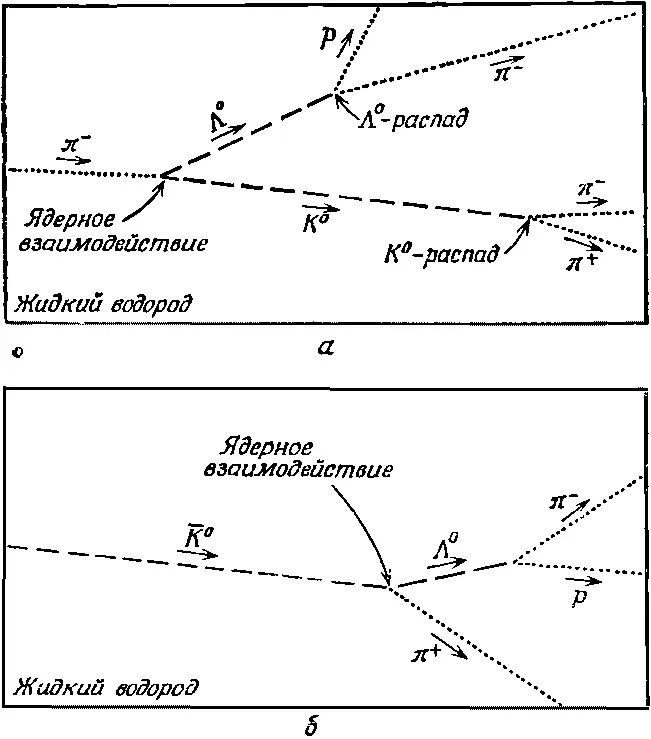
Фиг. 9.5. Высокоэнергетические события, наблюдаемые в водородной пузырьковой камере. а — π - -мезон взаимодействует с ядром водорода (протоном), образуя А 0 -частицу и К 0 -мезон; обе частицы распадаются в камере; б — — K 0 -мезон взаимодействует с протоном, образуя π - -мезон и А 0 -частицу, которая затем распадается. (Нейтральные частицы не оставляют следа. Предполагаемые их траектории показаны здесь штрихованными линиями.)

Когда К 0-мезон летит в веществе, он может провзаимодействовать с одним из ядер водорода (протонов), создав при этом, быть может, еще какие-то частицы. Предсказание теории странности состоит в том, что K 0-мезон никогда не породит Λ-частицу в простой реакции, скажем, такого типа

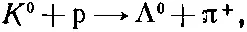
хотя — K 0-мезон это может сделать. Иначе говоря, в пузырьковой камере — K 0-мезон мог бы вызвать событие, показанное на фиг. 9.5, б, где Λ 0-частицу из-за распада можно заметить, а К 0-мезон не смог бы. Это первая часть рассказа. Это и есть сохранение странности.

Странность, впрочем, сохраняется не совсем . Существуют очень медленные распады странных частиц — распады, происходящие за большое время — порядка 10 -10 сек [36] Типичное время для сильного взаимодействия ближе к 10 -23 сек. , в которых странность не сохраняется. Их называют «слабые» распады. Например, K 0-мезон распадается на пару π-мезонов (+ и -) со временем жизни 10 -10 сек . Именно так на самом деле впервые были замечены K -частицы. Обратите внимание, что распадная реакция

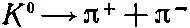
не сохраняет странности, так что «быстро», путем сильного взаимодействия, она идти не может. Может она идти только через слабый распадный процесс.

Далее, — K 0-мезон также распадается таким же путем (на π +и π -) и тоже с таким же самым временем жизни:

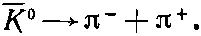
Здесь опять идет слабый распад, потому что он не сохраняет странности. Существует принцип, по которому для всякой реакции всегда найдется соответствующая реакция, в которой «материя» заменяется «антиматерией» и наоборот. Раз — K 0— это античастица К 0, она обязана распадаться на античастицы π +и π -, но античастица π +есть π -. (Или, если вам угодно, наоборот. Оказывается, что для π-мезонов неважно, кого из них назовут «материей», их эта материя совсем не интересует.) Итак, как следствие слабых распадов К 0- и — K 0-мезоны могут превращаться в одинаковые конечные продукты. Если «видеть» их по их распадам (как в пузырьковой камере), то выглядят они, как совершенно одинаковые частицы. Отличаются только их сильные взаимодействия.

Теперь наконец-то мы доросли до того, чтобы описать работу Гелл-Манна и Пайса. Во-первых, они отметили, что раз К 0и — K 0оба могут превращаться в два π-мезонов, то должна также существовать некоторая амплитуда того, что К 0может превратиться в К 0, и такая же амплитуда того, что — K 0превратится в К 0. Реакцию можно записать так, как это делают химики:

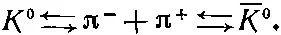(9.43)

Из существования таких реакций следует, что есть амплитуда, которую мы обозначим через -i/ ℏ < — K 0| W | K 0>, превращения К 0в — K 0, обусловленная тем самым слабым взаимодействием, с которым связан распад на два π-мезона. Ясно, что есть и амплитуда обратного процесса < K 0| W | — K 0>. Так как материя и антиматерия ведут себя одинаково, то эти две амплитуды численно равны между собой; мы обозначим их через А :

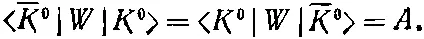(9.44)

И вот, сказали Гелл-Манн и Пайс, здесь возникает интересная ситуация. То, что люди назвали двумя разными состояниями мира ( К 0и — K 0), на самом деле следует рассматривать как одну систему с двумя состояниями, потому что имеется амплитуда перехода из одного состояния в другое. Для полноты рассуждений следовало бы, конечно, рассмотреть не два состояния, а больше, потому что существуют еще состояния 2π и т. д.; но поскольку наши физики интересовались главным образом связью К 0с — K 0, то они не захотели усложнять положения и представили его приближенно в виде системы с двумя состояниями. Другие состояния были учтены в той мере, в какой их влияние неявно скажется на амплитудах (9.44).

В соответствии с этим Гелл-Манн и Пайс анализировали нейтральную частицу как систему с двумя состояниями. Начали они с того, что выбрали состояния | К 0> и | — K 0> за базисные состояния. (С этого места весь рассказ становится очень похожим на то, что было для молекулы аммиака.) Всякое состояние |ψ> нейтрального K -мезона можно тогда описать, задав амплитуды того, что оно окажется в одном из базисных состояний. Обозначим эти амплитуды

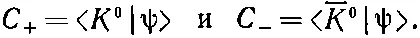(9.45)

Следующим шагом мы должны написать уравнение Гамильтона для такой системы с двумя состояниями. Если бы К 0и — K 0не были бы связаны между собой, то уравнения выглядели бы просто

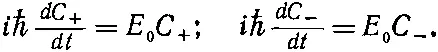(9.46)

Однако есть еще амплитуда < — K 0| W | K 0> перехода К 0в — K 0; поэтому в правую часть первого уравнения надо еще добавить слагаемое

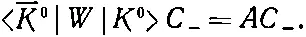
Аналогичное слагаемое АС +надо добавить и в уравнение, определяющее скорость изменения С -. Но это еще не все! Если уж мы учитываем двухпионный эффект, то надо учесть и то, что существует еще дополнительная амплитуда превращения К 0в самого себя по цепочке