Ричард Фейнман - Том 3. Квантовая механика

Мы покончили с системами с двумя состояниями, рассказав все, что хотелось. В дальнейших главах мы перейдем к изучению систем с большим числом состояний. Расширение на системы с N состояниями идей, разработанных для двух состояний, проходит довольно просто. Это делается примерно так.

Если система обладает N различными состояниями, то всякое состояние |ψ( t )> можно представить как линейную комбинацию произвольной совокупности базисных состояний | t >, где i =1, 2, 3, ..., N :

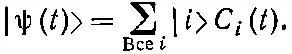(9.57)

Коэффициенты C i ( t ) — это амплитуды < i |ψ( t )>. Поведение амплитуд С i во времени направляется уравнениями

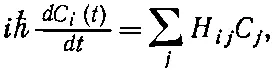(9.58)

где энергетическая матрица H ij описывает физику задачи. С виду она такая же, как и для двух состояний. Но только теперь и i , и j должны пробегать по всем N базисным состояниям, и энергетическая матрица H ij (или, если вам больше нравится, гамильтониан) — это теперь матрица N × N , состоящая из N 2чисел. Как и прежде, H ij = H ji (до тех пор, пока частицы сохраняются) и диагональные элементы H ii суть вещественные числа.

Мы нашли общее решение для всех С в системе с двумя состояниями, когда энергетическая матрица постоянна (не зависит от t ). Точно так же нетрудно решить и уравнение (9.58) для системы с N состояниями, когда Н не зависит от времени. Опять мы начинаем с того, что ищем возможное решение, в котором у всех амплитуд зависимость от времени одинакова . Мы пробуем

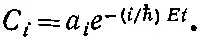(9.59)

Если все эти C i подставить в (9.58), то производные dC i ( t )/ dt превращаются просто в (- i / ℏ ) EC i . Сокращая повсюду на общую экспоненту, получаем

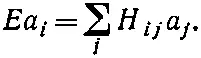(9.60)

Эта система N линейных алгебраических уравнений для N неизвестных a 1 а 2, ..., а n ; решение у нее бывает только тогда, когда вам сильно повезет, когда определитель из коэффициентов при всех а равен нулю. Но не нужно чересчур умничать: можете просто начать их решать любым способом, и вы сразу увидите, что решить их удается лишь при некоторых значениях E . (Вспомните, что единственная величина, которая в этих уравнениях подлежит подгонке, это Е .)

Если, впрочем, вы хотите, чтобы все было по форме, перепишите (9.60) так:

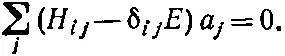(9.61)

Затем примените правило (если оно вам знакомо), что эти уравнения будут иметь решения лишь для тех значений Е , для которых

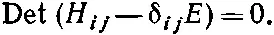(9.62)

Каждый член в детерминанте — это просто H ij и только из диагональных отнято Е . Иначе говоря, (9.62) означает просто

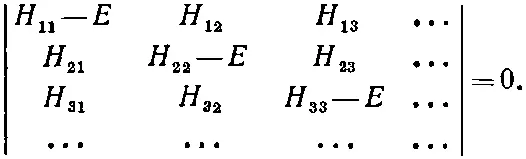(9.63)

Это, конечно, всего-навсего особый способ записывать алгебраические уравнения для Е , складывая вереницы членов, перемножаемых в определенном порядке. Эти произведения дадут все степени Е вплоть до E N .

Значит, у нас есть многочлен N -й степени, который равняется нулю. У него, вообще говоря, есть N корней. (Нужно помнить, однако, что некоторые из них могут быть кратными корнями; это значит, что два или более корней могут быть равны друг другу.) Обозначим эти N корней так:

(9.64)

(пусть n обозначает n - е порядковое числительное, так что n принимает значения I,II , ..., N). Некоторые из этих энергий могут быть между собой равны, скажем Е II = Е III , но мы решили все же обозначать их разными именами.

Уравнения (9.60) или (9.61) имеют по одному решению для каждого значения Е [из (9.64)]. Если вы подставите любое из Е , скажем E n , в (9.60) и найдете все а i , то получится ряд чисел а i , относящихся к энергии E n . Этот ряд мы обозначим а i ( n ).

Если подставить эти а i ( n ) в (9.59), то получатся амплитуды С i ( n ) того, что состояния с определенной энергией находятся в базисном состоянии | i >. Пусть | n > обозначает вектор состояния для состояния с определенной энергией при t =0. Тогда можно написать

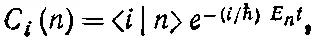
где

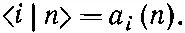(9.65)

Полное состояние с определенной энергией |ψ n( t )> можно тогда записать так:

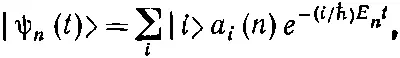
или

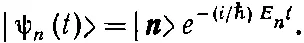(9.66)

Векторы состояний | n > описывают конфигурацию состояний с определенной энергией, но с вынесенной зависимостью от времени. Это постоянные векторы, которые, если мы захотим, можно использовать в качестве новой базисной совокупности.

Каждое из состояний | n > обладает тем свойством (в чем легко убедиться), что при действии на него оператором Гамильтона Н получится просто Е n , умноженное на то же состояние:

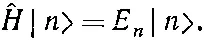(9.67)

Значит, энергия Е n — это характеристическое число оператора Гамильтона ^ Н . Как мы видели, у гамильтониана в общем случае бывает несколько характеристических энергий. Физики обычно называют их «собственными значениями» матрицы Н . Для каждого собственного значения ^ Н , иными словами, для каждой энергии, существует состояние с определенной энергией, которое мы называли «стационарным». Состояния | n > обычно именуются «собственными состояниями ^ Н ». Каждое собственное состояние отвечает определенному собственному значению Е n .