Ричард Фейнман - Том 3. Квантовая механика

Через минуту вы это узнаете. Но прежде хочу вам напомнить одну вещь: всякое состояние всегда можно представить в виде линейной комбинации базисных состояний. Для любого состояния |ψ|> можно написать

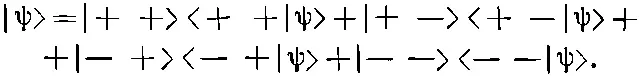(10.2)

Напомним, что полные скобки — это просто комплексные числа, так что их можно обозначить обычным образом через С i , где i =1, 2, 3 или 4, и записать (10.2) в виде

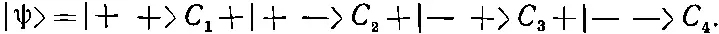(10.3)

Задание четверки амплитуд С i полностью описывает спиновое состояние |ψ>. Если эта четверка меняется во времени (как это и будет на самом деле), то скорость изменения во времени дается оператором ^ Н . Задача в том, чтобы найти этот оператор ^H.

Не существует общего правила, как писать гамильтониан атомной системы, и отыскание правильной формулы требует большего искусства, чем отыскание системы базисных состояний. Мы вам смогли дать общее правило, как записывать систему базисных состояний для любой задачи, в которой есть протон и электрон, но описать общий гамильтониан такой комбинации на этом уровне слишком трудно. Вместо этого мы подведем вас к гамильтониану некоторыми эвристическими рассуждениями, и вам придется признать его правильным, потому что результаты будут согласовываться с экспериментальными наблюдениями.

Вспомните, что в предыдущей главе мы смогли описать гамильтониан отдельной частицы со спином 1/ 2, применив сигма-матрицы или в точности эквивалентные им сигма-операторы. Свойства операторов сведены в табл. 10.1.

Таблица 10.1. СВОЙСТВА СИГМА-ОПЕРАТОРОВ

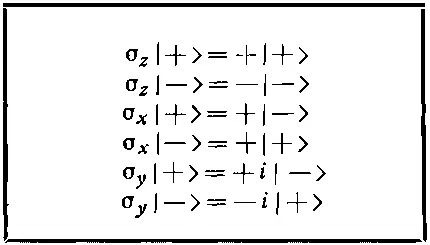
Эти операторы, являющиеся просто удобным, кратким способом запоминания матричных элементов типа <+|σ z|+>, были полезны для описания поведения отдельной частицы со спином 1/ 2. Возникает вопрос, можно ли отыскать аналогичное средство для описания системы с двумя спинами. Да, и очень просто. Вот смотрите. Мы изобретем вещь, которую назовем «электрон-сигма» и которую будем представлять векторным оператором σ eс тремя компонентами σ e x, σ e yи σ e z. Дальше условимся , что когда одна из них действует на какое-то из наших четырех базисных состояний атома водорода, то она действует на один только спин электрона, причем так, как если бы электрон был один, сам по себе. Пример: чему равно σ y е |-+>? Поскольку σ y, действующее на электрон со спином вниз, дает - i , умноженное на состояние с электроном, у которого спин вверх, то

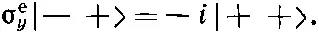
(Когда σ y едействует на комбинированное состояние, оно переворачивает электрон, не затрагивая протон, и умножает результат на - i .) Действуя на другие состояния, σ е у даст

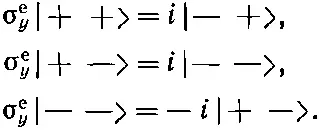
Напомним еще раз, что оператор σ едействует только на первый спиновый символ, т. е. на спин электрона .

Теперь определим соответствующий оператор «протон-сигма» для спина протона. Три его компоненты σ p x, σ p y, σ p z, действуют так же, как и σ е, но только на протонный спин . Например, если σ p xбудет действовать на каждое из четырех базисных состояний, то получится (опять с помощью табл. 10.1)

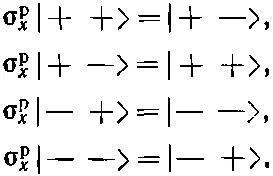
Как видите, ничего трудного.

В общем случае могут встретиться вещи и посложнее. Например, произведение операторов σ e yσ p z. Когда имеется такое произведение, то сначала делается то, что хочет правый оператор, а потом — чего требует левый [39] Для этих операторов, правда, оказывается, что от их порядка ничего не зависит. . Например,

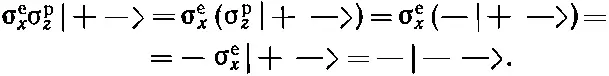
Заметьте, что эти операторы с числами ничего не делают; мы использовали это, когда писали σ e x(-1)=(-1) σ e x. Мы говорим, что операторы «коммутируют» с числами или что числа «можно протащить» через оператор. Попрактикуйтесь и покажите, что произведение σ е х σ p zдает для четырех состояний следующий результат:

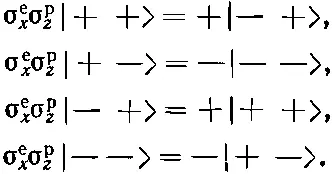
Если перебрать все допустимые операторы, каждый по разу, то всего может быть 16 возможностей. Да, шестнадцать , если включить еще «единичный оператор» 1. Во-первых, есть тройка σ е х , σ е y , σ е z , затем тройка σ p x, σ p y, σ p z, итого шесть. Кроме того, имеется девять произведений вида σ е х σ p y, итого 15. И еще единичный оператор, оставляющий все состояния нетронутыми. Вот и все шестнадцать!

Заметьте теперь, что для системы с четырьмя состояниями матрица Гамильтона должна представлять собой матрицу коэффициентов 4×4, в ней будет 16 чисел. Легко показать, что всякая матрица 4×4, и в частности матрица Гамильтона, может быть записана в виде линейной комбинации шестнадцати двойных спиновых матриц, соответствующих системе операторов, которые мы только что составили. Поэтому для взаимодействия между протоном и электроном, в которое входят только их спины, мы можем ожидать, что оператор Гамильтона может быть записан в виде линейной комбинации тех же 16 операторов. Вопрос только в том, как.

Но, во-первых, мы знаем, что взаимодействие не зависит от нашего выбора осей для системы координат. Если нет внешнего возмущения — чего-то вроде магнитного поля, выделяющего какое-то направление в пространстве, — то гамильтониан не может зависеть от нашего выбора направлений осей х, у и z . Это означает, что в гамильтониане не может быть таких членов, как σ e xсам по себе. Это выглядело бы нелепо, потому что кто-нибудь в другой системе координат пришел бы к другим результатам.

Единственно возможны только член с единичной матрицей, скажем постоянная а (умноженная на ^1), и некоторая комбинация сигм, которая не зависит от координат, некоторая «инвариантная» комбинация. Единственная скалярная инвариантная комбинация из двух векторов — это их скалярное произведение, имеющее для наших сигм вид

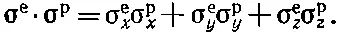(10.4)