Ричард Фейнман - Том 3. Квантовая механика

Вы, вероятно, уже слышали раньше о «21-см линии» водорода. Это и есть длина волны спектральной линии в 1420 Мгц между сверхтонкими состояниями. Излучение с такой длиной волны испускается или поглощается атомарным водородным газом в галактиках. Значит, с помощью радиотелескопов, настроенных на волны 21 см (или примерно на 1420 Мгц ), можно наблюдать скорости и расположение сгущений атомарного водорода. Измеряя интенсивность, можно оценить его количество. Измеряя сдвиг в частоте, вызываемый эффектом Допплера, можно выяснить движение газа в галактике. Это одна из великих программ радиоастрономии. Так что мы с вами сейчас ведем речь о чем-то очень реальном, это вовсе не какая-то искусственная задача.

Хотя с задачей отыскания уровней энергии основного состояния водорода мы и справились, мы все же продолжим изучение этой интересной системы. Чтобы сказать о ней еще что-то, например чтобы подсчитать скорость, с какой атом водорода поглощает или испускает радиоволны длиной 21 см , надо знать, что с ним происходит, когда он возмущен. Нужно проделать то, что мы сделали с молекулой аммиака, — после того как мы нашли уровни энергии, мы отправились дальше и выяснили, что происходит, когда молекула находится в электрическом поле. И после этого нетрудно оказалось представить себе влияние электрического поля радиоволны. В случае атома водорода электрическое поле ничего с уровнями не делает, разве что сдвигает их все на некоторую постоянную величину, пропорциональную квадрату поля, а нам это неинтересно, потому что это не меняет разностей энергий. На сей раз важно уже магнитное поле. Значит, следующим шагом будет написать гамильтониан для более сложного случая, когда атом сидит во внешнем магнитном поле.

Каков же этот гамильтониан? Мы просто сообщим вам ответ, потому что никакого «доказательства» дать не можем, разве что сказать, что именно так устроен атом.

Гамильтониан имеет вид

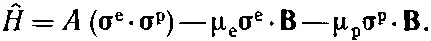(10.27)

Теперь он состоит из трех частей. Первый член А (σ е·σ р) представляет магнитное взаимодействие между электроном и протоном; оно такое же, как если бы магнитного поля не было. Влияние внешнего магнитного поля проявляется в остальных двух членах. Второй член (-μ е σ е · В) — это та энергия, которой электрон обладал бы в магнитном поле, если бы он там был один [43] Вспомните, что классически U=- μ · B , так что энергия наименьшая, когда момент направлен по полю. Для положительно заряженных частиц магнитный момент параллелен спину, для отрицательных — наоборот. Значит, в (10.27) μ р — число положительное, а μ е — отрицательное. . Точно так же последний член (-μ р σ р· В) был бы энергией протона-одиночки. Согласно классической физике, энергия их обоих вместе была бы суммой их энергий; по квантовой механике это тоже правильно. Возникающая из-за наличия магнитного поля энергия взаимодействия равна просто сумме энергий взаимодействия электрона с магнитным полем и протона с тем же полем, выраженных через операторы сигма. В квантовой механике эти члены в действительности не являются энергиями, но обращение к классическим формулам для энергии помогает запоминать правила написания гамильтониана. Как бы то ни было, (10.27) — это правильный гамильтониан.

Теперь нужно вернуться к началу и решать всю задачу сызнова. Но большая часть работы уже сделана, надо только добавить эффекты, вызываемые новыми членами. Примем, что магнитное поле Впостоянно и направлено по z . Тогда к нашему старому гамильтонову оператору ^ Н надо добавить два новых куска; обозначим их ^ Н ':

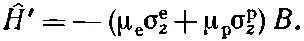
Пользуясь табл. 10.1, мы сразу получаем

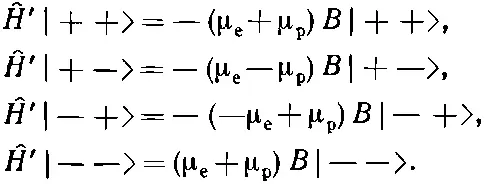(10.28)

Смотрите, как удобно! Оператор Н ', действуя на каждое состояние, дает просто число, умноженное на это же состояние. В матрице < i | H '| j > есть поэтому только диагональные элементы, и можно просто добавить коэффициенты из (10.28) к соответствующим диагональным членам в (10.13), так что гамильтоновы уравнения (10.14) обращаются в

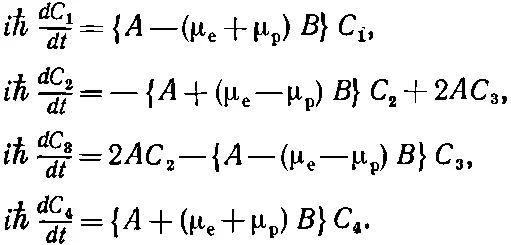(10.29)

Форма уравнений не изменилась, изменились только коэффициенты. И пока В не меняется со временем, можно все делать так же, как и раньше.

Подставляя C i = a i e -( i / ℏ ) Et , мы получаем

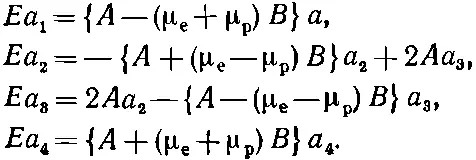(10.30)

К счастью, первое и четвертое уравнения по-прежнему не зависят от остальных, так что снова пойдет в ход та же техника. Одно решение — это состояние | I >, для которого

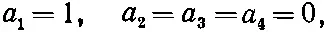
или

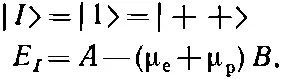(10.31)

Другое решение

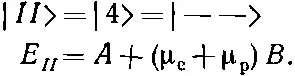(10.32)

Для остальных двух уравнений потребуется больше работы, потому что коэффициенты при а 2и a 3уже не равны друг другу. Но зато они очень похожи на ту пару уравнений, которую мы писали для молекулы аммиака. Оглядываясь на уравнения (7.20) и (7.21), можно провести следующую аналогию (помните, что тамошние индексы 1 и 2 соответствуют здесь индексам 2 и 3):

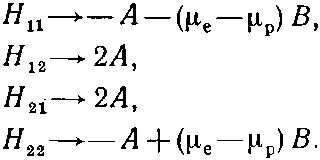(10.33)

Раньше энергии давались формулой (7.25), которая имела вид

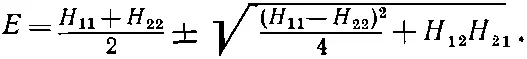(10.34)

Подставляя сюда (10.33), получаем для энергии

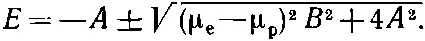
В гл. 7 мы привыкли называть эти энергии Е I и Е II , теперь мы их обозначим Е III и E IV :

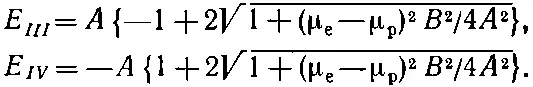(10.35)