Ричард Фейнман - Том 3. Квантовая механика
- Название:Том 3. Квантовая механика
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:неизвестен
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Ричард Фейнман - Том 3. Квантовая механика краткое содержание
Том 3. Квантовая механика - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
В атоме водорода мы с вами отыскали систему со спином 1, составленную из двух частиц со спином 1/ 2. В гл. 4 мы уже научились преобразовывать амплитуды для спина 1/ 2. Эти знания можно применить к тому, чтобы получить преобразование для спина 1. Вот как это делается: имеется система (атом водорода с энергией + А ) со спином 1. Пусть мы пропустили ее сквозь фильтр S Штерна—Герлаха так, что знаем теперь, что она находится в одном из базисных состояний по отношению к S , скажем в |+ S >. Какова амплитуда того, что она окажется в одном из базисных состояний, скажем |+ T >, по отношению к прибору Т ? Если вы назовете систему координат прибора S системой х, у, z , то состояние |+ S > — это то, что недавно называлось состоянием |++>. Но представьте, что какой-то ваш приятель провел свою ось z вдоль оси Т . Он свои состояния будет относить к некоторой системе х ', у ', z'. Его состояния «вверх» и «вниз» для электрона и протона отличались бы от ваших. Его состояние «плюс — плюс», которое можно записать |+'+'>, отмечая «штрихованность» системы, есть состояние |+ Т > частицы со спином 1. А вас интересует <+ T |+ S >, что есть просто иной способ записи амплитуды <+'+'|++>.
Амплитуду <+'+'|++> можно найти следующим образом. В вашей системе спин электрона из состояния |++> направлен вверх. Это означает, что у него есть некоторая амплитуда <+'|+> eоказаться в системе вашего приятеля спином вверх и некоторая амплитуда <-'|+> еоказаться в этой системе спином вниз. Равным образом, протон в состоянии |++> имеет спин вверх в вашей системе и амплитуды <+'|+> ри <-'|+> pоказаться спином вверх или вниз в «штрихованной» системе. Поскольку мы говорим о двух разных частицах, то амплитуда того, что обе частицы вместе в его системе окажутся спинами вверх, равна произведению амплитуд
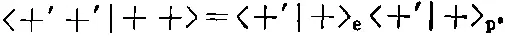 (10.44)
(10.44)
Мы поставили значки е и р под амплитудами <+'|+>, чтоб было ясно, что мы делаем. Но обе они — это просто амплитуды преобразований для частицы со спином 1/ 2, так что на самом деле — это одни и те же числа. Фактически — это те же амплитуды, которые мы в гл. 4 называли <+ Т |+ S > и которые мы привели в табл. 4.1 и 4.2.
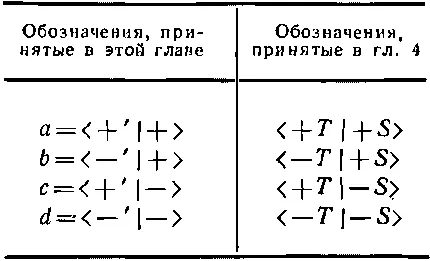
Но теперь, однако, нам угрожает путаница в обозначениях. Надо уметь различать амплитуду <+ T |+ S > для частицы со спином 1/ 2от того, что мы также назвали <+ T |+ S >, но для спина 1—между ними нет ничего общего! Надеюсь, вас не очень собьет с толку, если мы на время введем иные обозначения амплитуд для спина 1/ 2. Они приведены в табл. 10.4. Для состояний частиц спина 1 мы по-прежнему будем прибегать к обозначениям |+ S >, |0 S > и |- S >.
Таблица 10.4. АМПЛИТУДЫ для СПИНА 1/ 2
В наших новых обозначениях (10.44) просто превращается в
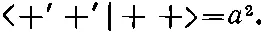
Это как раз амплитуда <+ T |+ S > для спина 1. Теперь давайте, например, предположим, что у вашего приятеля система координат, т. е. «штрихованный» прибор Т , повернута вокруг вашей оси z на угол φ; тогда из табл. 4.2 получается
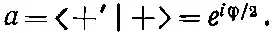
Значит, из (10.44) амплитуда для спина 1 окажется равной
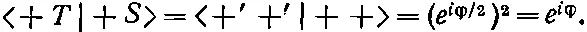 (10.45)
(10.45)
Теперь вам понятно, как мы будем действовать дальше.
Но хорошо бы провести выкладки в общем случае для всех состояний. Если протон и электрон в нашей системе (системе S ) оба смотрят вверх, то амплитуды того, что в другой системе (системе Т ) они будут в одном из четырех возможных состояний, равны
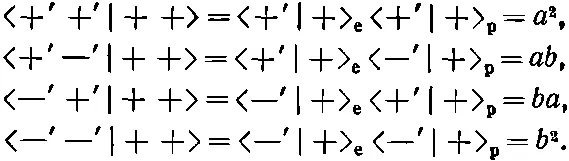 (10.46)
(10.46)
Затем мы можем записать состояние |++> в виде следующей линейной комбинации:
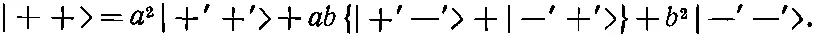 (10.47)
(10.47)
Но теперь мы замечаем, что |+'+'> — это состояние |+ Т >, что {|+ '-'> + |-'+'>} — это как раз √2, умноженный на состояние |0 T > [см. (10.41)], и что |-'-'>=|- Т >. Иными словами, (10.47) переписывается в виде
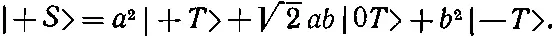 (10.48)
(10.48)
Точно так же легко показать, что
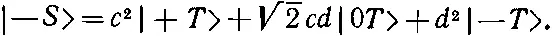 (10.49)
(10.49)
С |0 S > дело обстоит чуть посложнее, потому что
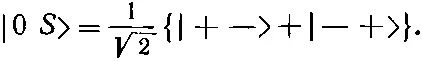
Но каждое из состояний |+-> и |-+> можно выразить через «штрихованные» состояния и подставить в сумму:
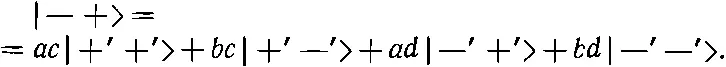 (10.50)
(10.50)
и
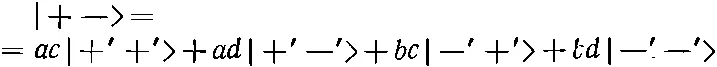 (10.51)
(10.51)
Умножая сумму (10.50) и (10.51) на 1/√2, получаем
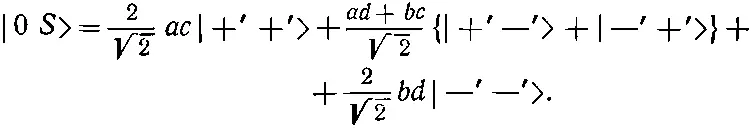
Отсюда следует
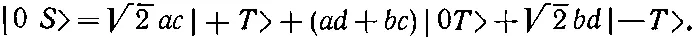 (10.52)
(10.52)
Теперь у нас есть все необходимые амплитуды. Коэффициенты в (10.48), (10.49) и (10.52) —это матричные элементы < jТ | iS >. Сведем их в одну матрицу:
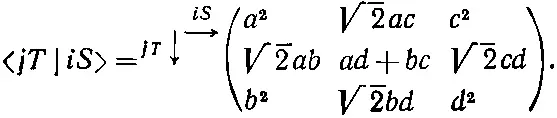 (10.53)
(10.53)
Мы выразили преобразование спина 1 через амплитуды а, b , с и d преобразования спина 1/ 2.
Если, например, система Т повернута по отношению к S на угол α вокруг оси у (см. фиг. 3.6, стр. 64), то амплитуды в табл. 10.4—это просто матричные элементы R y (α) в табл. 4.2:
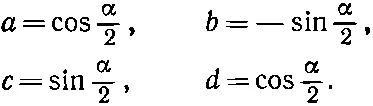 (10.54)
(10.54)
Подставив их в (10.53), получим формулы (3.38), которые приведены на стр. 80 без доказательства.
Но что же случилось с состоянием | IV> ?! Это система со спином нуль; значит, у нее есть только одно состояние — оно во всех системах координат одно и то же. Можно проверить, что все так и выходит, если взять разность (10.50) и (10.51); получим
Читать дальшеИнтервал:
Закладка:






