Ричард Фейнман - Том 3. Квантовая механика

«Погодите минутку, — вероятно, скажете вы.— «Состояния | III > и | IV > — это не состояния |+-> и |-+>; они являются их смесями ». Верно, но перемешивание здесь едва заметно. Действительно, при B=0 они являются смесями, но мы пока не выясняли, что бывает при больших В . Когда мы для получения энергии стационарных состояний пользовались аналогией между (10.33) и формулами гл. 7, то заодно можно было оттуда взять и амплитуды. Они получатся из (7.23):

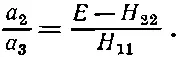
Отношение a 2/ a 3— это, конечно, на сей раз C 2/ C 3Вставляя аналогичные величины из (10.33), получаем

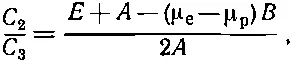
или

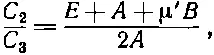(10.39)

где вместо Е надо взять подходящую энергию (либо Е III , либо E IV ). Например, для состояния | III > имеем

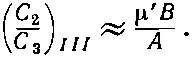(10.40)

Значит, при больших В у состояния | III > С 2≫ С 3; состояние почти полностью становится состоянием |2>=|+->. Точно так же если в (10.39) подставить E IV , то получится, что (С 2/С 3) IV≪1; в сильных полях состояние | IV > обращается попросту в состояние |3>=|-+>. Вы видите, что коэффициенты в линейных комбинациях наших базисных состояний, составляющих стационарные состояния, сами зависят от В . Состояние, которое мы именуем | III >, в очень слабых полях представляет собой смесь |+-> и |-+> в пропорции 1:1, но в сильных полях целиком смещается к |+->. Точно так же и состояние | IV >, которое в слабых полях также является смесью |+-> и |-+> в пропорции 1:1 (с обратным знаком), переходит в состояние |-+>, когда спины из-за сильного внешнего поля больше друг с другом не связаны.

Хотелось бы обратить ваше внимание, в частности, на то, что происходит в очень слабых магнитных полях. Имеется одна энергия (-3 А ), которая не изменяется при включении слабого магнитного поля. И имеется другая энергия (+ А ), которая при включении слабого магнитного поля расщепляется на три различных уровня энергии. В слабых полях энергии с ростом В меняются так, как показано на фиг. 10.5.

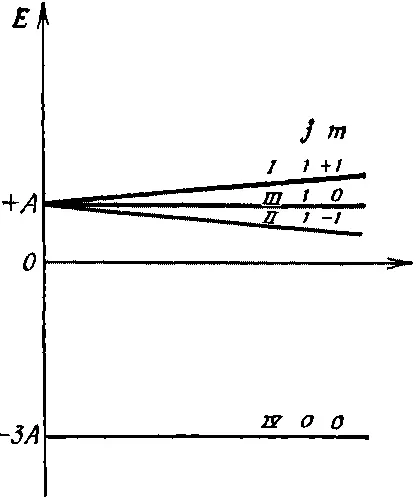
Фиг. 10.5. Состояния атома водорода в слабых магнитных полях.

Допустим, что у нас есть каким-то образом отобранное множество атомов водорода, у которых у всех энергия равна -3 А . Если пропустить их через прибор Штерна—Герлаха (с не очень сильными полями), то мы найдем, что они просто проходят целиком насквозь. (Поскольку их энергия не зависит от В , то, согласно принципу виртуальной работы, градиент магнитного поля не создает никакой силы, которая бы ощущалась ими.) Пусть, с другой стороны, мы бы отобрали группку атомов с энергией + А и пропустили их через прибор Штерна—Герлаха, скажем через прибор S . (Опять поля в приборе не должны быть столь сильными, чтобы разрушить внутренность атома; подразумевается, что поля малы настолько, что энергии можно считать линейно зависящими от В .) Мы бы получили три пучка . На состояния | I > и | II > действуют противоположные силы, их энергии меняются по В линейно с наклоном ±μ, так что силы сходны с силами, действующими на диполь, у которого μ z =±μ, а состояние | III > проходит насквозь. Мы опять возвращаемся к гл. 3. Атом водорода с энергией + А — это частица со спином 1. Это энергетическое состояние является «частицей», для которой j =1, и может быть описано (по отношению к некоторой системе осей в пространстве) в терминах базисных состояний |+ S >, |0 S > и |- S >, которыми мы пользовались в гл. 3. С другой стороны, когда атом водорода имеет энергию -3 А , он является частицей со спином нуль. (Напоминаем, что все сказанное, строго говоря, справедливо лишь для бесконечно малых магнитных полей.) Итак, состояния водорода в нулевом магнитном поле можно сгруппировать следующим образом:

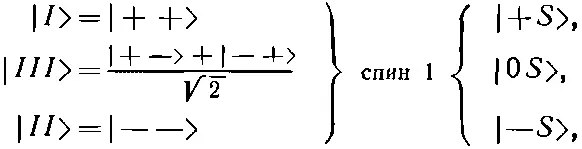(10.41)

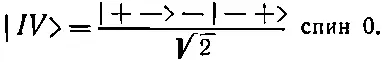(10.42)

В гл. 35 (вып. 7) мы говорили, что у всякой частицы компоненты момента количества движения вдоль любой оси могут принимать только определенные значения, всегда отличающиеся на ℏ . Так, z-компонента момента количества движения J z может быть равна jℏ , (j-1) ℏ , ( j -2) ℏ ,..., (- j ) ℏ , где j — спин частицы (который может быть целым или полуцелым). Обыкновенно пишут

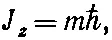(10.43)

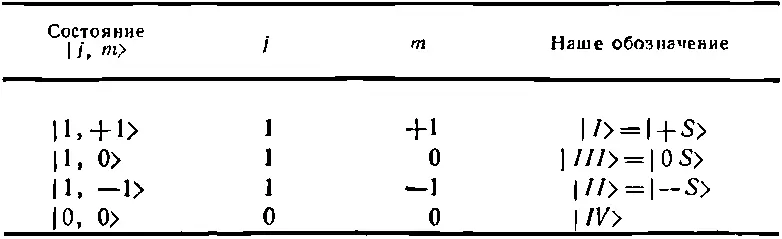
где m стоит вместо любого из чисел j, j -1, j -2, ...,- j (в свое время мы не сказали об этом). Вы поэтому часто встретите в книжках нумерацию четырех основных состояний при помощи так называемых квантовых чисел j и m [часто именуемых «квантовым числом полного момента количества движения» ( j ) и «магнитным квантовым числом» ( m )]. Вместо наших символов состояний | I >, | II > и т. д. многие часто пишут состояния в виде | j, m >. Нашу табличку состояний для нулевого поля в (10.41) и (10.42) они бы изобразили в виде табл. 10.3. Здесь нет какой-либо новой физики, это просто вопрос обозначении.

Таблица 10.3. СОСТОЯНИЯ АТОМА ВОДОРОДА В НУЛЕВОМ ПОЛЕ

Теперь мы хотели бы применить наши знания об атоме водорода к одной специальной задаче. В гл. 3 мы говорили о том, что частица со спином 1, находящаяся в одном из базисных состояний (+, 0, -) по отношению к прибору Штерна—Герлаха с какой-то частной ориентацией (скажем, по отношению к прибору S ), будет иметь определенную амплитуду пребывания в одном из трех состояний по отношению к прибору Т , ориентированному в пространстве по-другому. Имеются девять таких амплитуд < jT | iS >, которые вместе образуют проекционную матрицу. В гл. 3, § 7, мы без доказательства выписали элементы этой матрицы для различных ориентации Т по отношению к S . Теперь мы хотим показать вам один из способов их вывода.