Ричард Фейнман - Том 3. Квантовая механика

«Взгляните, — сказал Дирак, — первое и последнее уравнения я могу записать также в виде

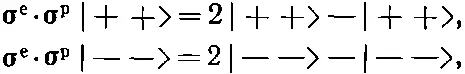
и тогда все они станут похожими. Теперь я придумаю новый оператор, который обозначу Р спин. обмени который, по определению , будет обладать следующими свойствами [40] Этот оператор сейчас называют оператор обмена спинами. :

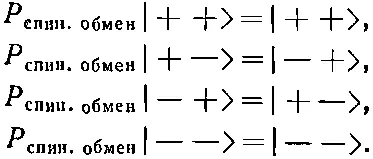
Оператор этот, как видите, только обменивает направления спина у двух частиц. Тогда всю систему уравнений (10.15) я могу написать как одно простое операторное уравнение:

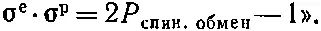(10.16)

Это и есть формула Дирака. Оператор обмена спинами дает удобное правило для запоминания σ е ·σ p . (Как видите, вы теперь уже все умеете делать. Для вас все двери открыты.)

Теперь мы готовы к тому, чтобы вычислить уровни энергии основного состояния водорода, решая гамильтоновы уравнения (10.14). Мы хотим найти энергии стационарных состояний. Это значит, что мы должны отыскать те особые состояния |ψ>, для которых каждая из принадлежащих |ψ> амплитуд C i =< i |ψ> обладает одной и той же зависимостью от времени, а именно е -ω t . Тогда состояние будет обладать энергией E = ℏ ω. Значит, мы ищем совокупность амплитуд, для которых

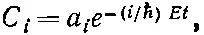(10.17)

где четверка коэффициентов а i не зависит от времени. Чтобы увидеть, можем ли мы получить эти амплитуды, подставим (10.17) в (10.14) и посмотрим, что из этого выйдет. Каждое iℏdC i / dt в (10.14) перейдет в EC i . И после сокращения на общий экспоненциальный множитель каждое С i превратится в а i ; получим

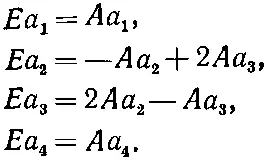(10.18)

Это и нужно решить для отыскания a 1, а 2, а 3и а 4. Право, очень мило со стороны первого уравнения, что оно не зависит от остальных, — а это значит, что одно решение сразу видно. Если выбрать Е = А , то

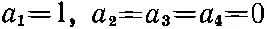
даст решение. (Конечно, если принять все а равными нулю, то это тоже будет решение, но состояния оно не даст!) Будем считать наше первое решение состоянием [41] В действительности состоянием является но, как обычно, мы отождествим состояния с постоянными векторами, которые при t=0 совпадают с настоящими векторами. | I >:

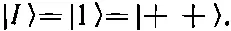(10.19)

Его энергия

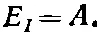
Все это немедленно дает ключ ко второму решению, получаемому из последнего уравнения в (10.18):

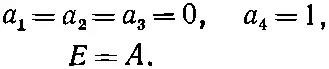
Это решение мы назовем состоянием | II >:

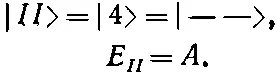(10.20)

Дальше пойдет чуть труднее; оставшиеся два уравнения (10.18) переплетены одно с другим. Но мы все это уже делали. Сложив их, получим

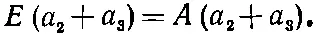(10.21)

Вычитая, будем иметь

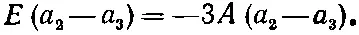(10.22)

Окидывая это взглядом и припоминая знакомый нам уже аммиак, мы видим, что здесь есть два решения:

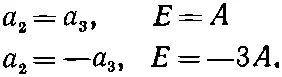(10.23)

Это смеси состояний |2> и |3>. Обозначая их | III > и | IV > и вставляя для правильной нормировки множитель 1/√2, имеем

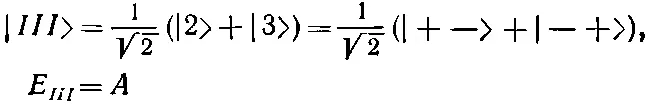(10.24)

и

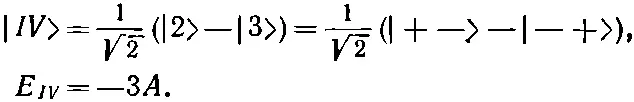(10.25)

Мы нашли четверку стационарных состояний и их энергии. Заметьте, кстати, что наши четыре состояния ортогональны друг другу, так что их тоже можно при желании считать базисными состояниями. Задача наша полностью решена.

У трех состояний энергия равна А , а у последнего -3 А . Среднее равно нулю, а это означает, что когда в (10.5) мы выбрали Е 0=0, то тем самым мы решили отсчитывать все энергии от их среднего значения. Диаграмма уровней энергии основного состояния водорода будет выглядеть так, как на фиг. 10.2.

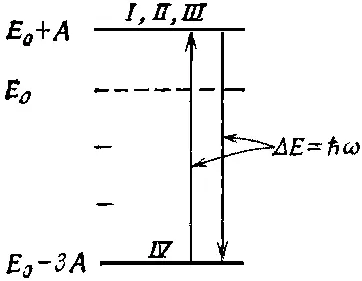
Фиг. 10.2. Диаграмма уровней энергии основного состояния атомарного водорода.

Различие в энергиях между состоянием | IV > и любым из остальных равно 4 A . Атом, который случайно окажется в состояний | I >, может оттуда упасть в состояние | IV > и испустить свет: не оптический свет, потому что энергия очень мала, а микроволновой квант. Или, если осветить водородный газ микроволнами, мы заметим поглощение энергии, оттого что атомы в состоянии | IV > будут ее перехватывать и переходить в одно из высших состояний, но все это только на частоте ω=4 A /ℏ. Эта частота была измерена экспериментально; наилучший результат, полученный сравнительно недавно [42] Crampton, Kleppner, Ramsey, Physical Review Letters, 11, 338 (1963). , таков:

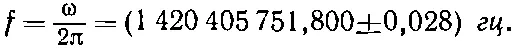(10.26)

Ошибка составляет только три стомиллиардных! Вероятно, ни одна из фундаментальных физических величин не измерена лучше, чем эта; таково одно из наиболее выдающихся по точности измерений в физике. Теоретики были очень счастливы, когда им удалось вычислить энергию с точностью до 3·10 -5; но к этому времени она была измерена с точностью до 2·10 -11,т.е. в миллион раз точнее, чем в теории. Так что экспериментаторы идут далеко впереди теоретиков. В теории основного состояния атома водорода и вы , и мы находимся в одинаковом положении. Вы ведь тоже можете взять значение А из опыта — и всякому, в конце концов, приходится делать то же самое.