Ричард Фейнман - Том 3. Квантовая механика

Итак, мы нашли энергии четырех стационарных состояний атома водорода в постоянном магнитном поле. Проверим наши выкладки, для чего устремим В к нулю и посмотрим, получатся ли те же энергии, что и в предыдущем параграфе. Вы видите, что всё в порядке. При В =0 энергии Е I , Е II и Е III обращаются в + А, а E IV — в -3 А . Даже наша нумерация состояний согласуется с прежней. Но когда мы включим магнитное поле, то каждая энергия начнет меняться по-своему. Посмотрим, как это происходит.

Во-первых, напомним, что у электрона μ еотрицательно и почти в 1000 раз больше μ р, которое положительно. Значит, и μ e+μ p, и μ e-μ pоба отрицательны и почти равны друг другу. Обозначим их -μ и -μ':

(10.36)

(И μ, и μ' положительны и по величине почти совпадают с μ е, которое примерно равно одному магнетону Бора.) Наша четверка энергий тогда обратится в

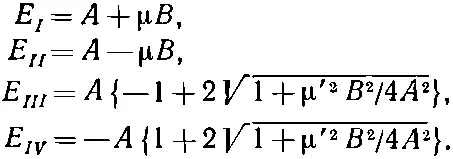(10.37)

Энергия Е I вначале равна А и линейно растет с ростом В со скоростью μ. Энергия Е II тоже вначале равна A , но с ростом В линейно убывает , наклон ее кривой равен -μ. Изменение этих уровней с В показано на фиг. 10.3. На рисунке показаны также графики энергий Е III и E IV . Их зависимость от В иная. При малых В они зависят от В квадратично; вначале наклон их равен нулю, а затем они начинают искривляться и при больших В приближаются к прямым с наклоном ±μ', близким к наклону E I и Е II

Сдвиг уровней энергии атома, вызываемый действием магнитного поля, называется эффектом Зеемана . Мы говорим, что кривые на фиг. 10.3 показывают зеемановское расщепление основного состояния водорода.

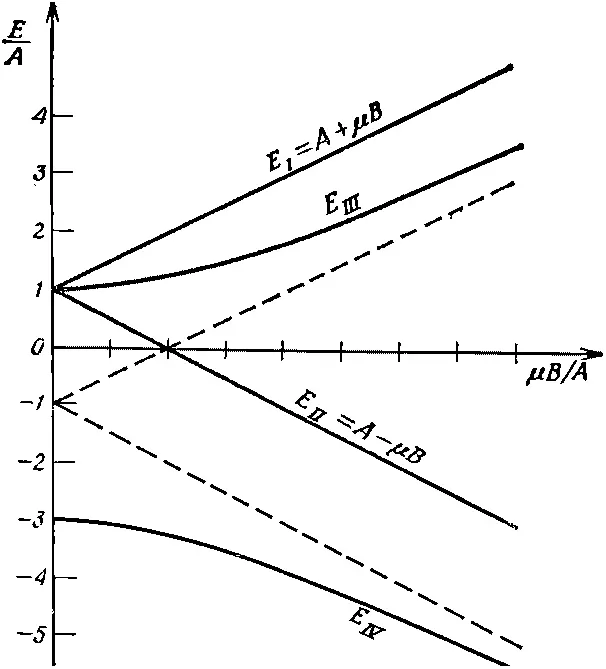
Фиг. 10.3. Уровни энергии основного состояния водорода в магнитном поле В. Кривые E III и Е IV приближаются к пунктирным прямым А±μ'В.

Когда магнитного поля нет, то просто получается одна спектральная линия от сверхтонкой структуры водорода. Переходы между состоянием | IV > и любым из остальных трех происходят с поглощением или испусканием фотона, частота которого равна 1420 Мгц : 1/ ℏ , умноженной на разность энергий 4 A . Но когда атом находится в магнитном поле В, то линий получается гораздо больше. Могут происходить переходы между любыми двумя из четырех состояний. Значит, если мы имеем атомы во всех четырех состояниях, то энергия может поглощаться (или излучаться) в любом из шести переходов, показанных на фиг. 10.4 вертикальными стрелками.

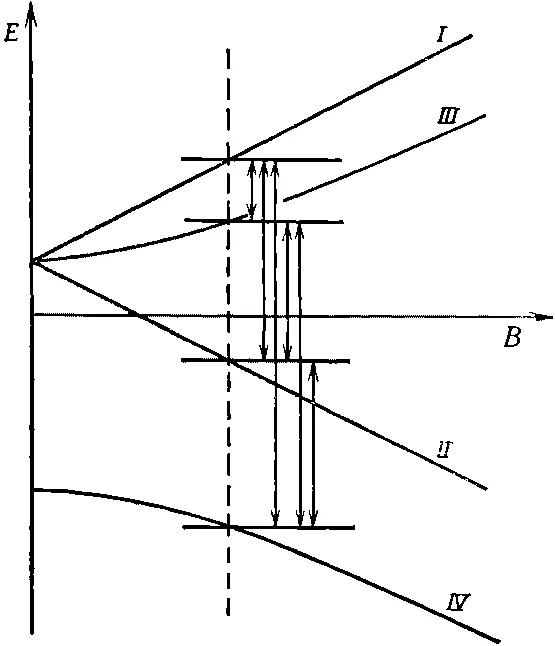
Фиг. 10.4. Переходы между уровнями энергии основного состояния водорода в некотором магнитном поле В.

Многие из этих переходов можно наблюдать с помощью техники молекулярных пучков Раби, которую мы описывали в гл. 35, § 3 (вып.7).

Что же является причиной переходов? Они возникают, если наряду с сильным постоянным полем B приложить малое возмущающее магнитное поле, которое меняется во времени. То же самое мы наблюдали и при действии переменного электрического поля на молекулу аммиака. Только здесь виновник переходов — это магнитное поле, действующее на магнитные моменты. Но теоретические выкладки те же самые, что и в случае аммиака. Проще всего они получаются, если взять возмущающее магнитное поле, вращающееся в плоскости ху , хотя то же будет от любого осциллирующего горизонтального поля. Если вы вставите это возмущающее поле в качестве добавочного члена в гамильтониан, то получите решения, в которых амплитуды меняются во времени, как это было и с молекулой аммиака. Значит, вы сможете легко и аккуратно рассчитать вероятность перехода из одного состояния в другое. И обнаружите, что все это согласуется с опытом.

Теперь займемся формой кривых на фиг. 10.3. Во-первых, если говорить о больших полях, то зависимость энергии от поля довольно интересна и легко объяснима. При достаточно больших В (а именно при μ B / A ≫1) в формулах (10.37) можно пренебречь единицей. Четверка энергий принимает вид

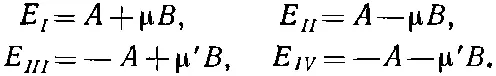(10.38)

Это уравнения четырех прямых на фиг. 10.3. Эти формулы можно физически понять следующим образом. Природа стационарных состояний в нулевом поле полностью определяется взаимодействием двух магнитных моментов. Перемешивание базисных состояний |+-> и |-+> в стационарных состояниях |III> и | IV > вызвано этим взаимодействием. Однако вряд ли можно ожидать, что каждая из наших частиц (и протон, и электрон) в сильных внешних полях будет испытывать влияние поля другой частицы; каждая будет действовать так, как если бы во внешнем поле находилась она одна. Тогда (как мы уже много раз видели) спин электрона окажется направленным вдоль внешнего магнитного поля (по нему или против него).

Пусть спин электрона направлен вверх, т. е. вдоль поля; энергия его будет -μ e B . Протон при этом может стоять по-разному. Если у него спин тоже направлен вверх, то его энергия -μ p B . Их сумма равна -(μ е+μ р) B =μ B . А это как раз и есть E I , и это очень приятно, потому что мы описываем состояние |++>=| I >. Есть еще небольшой дополнительный член А (теперь (μ B ≫ A ), представляющий энергию взаимодействия протона и электрона, когда их спины параллельны. (Мы с самого начала считали А положительным, потому что так должно было быть по теории, о которой шла речь; то же получается и на опыте.) Но спин протона может быть направлен и вниз. Тогда его энергия во внешнем поле обратится в +μ Р B , а вместе с электроном их энергия будет -(μ e-μ р) В =μ В . А энергия взаимодействия обращается в - А . Их сумма даст энергию Е III , в (10.38). Так что состояние | III > в сильных полях становится состоянием |+->.

Пусть теперь спин электрона направлен вниз. Его энергия во внешнем поле равна μ e В . Если и протон смотрит вниз, то их общая энергия равна (μ e+μ p) В =-μ В плюс энергия взаимодействия А (спины-то теперь параллельны). Это приводит как раз к энергии Е II в (10.38) и соответствует состоянию |-->=| II >, что очень мило. И наконец, если у электрона спин направлен вниз, а у протона — вверх, то мы получим энергию (μ e-μ p ) В - А ( минус А потому, что спины противоположны), т. е. E IV . А состояние отвечает |-+>.