Ричард Фейнман - Том 3. Квантовая механика

Далее, состояния | n > (их N штук) могут, вообще говоря, тоже быть выбраны в качестве базиса. Для этого все состояния должны быть ортогональны в том смысле, что для любой пары их, скажем | n > и | m >,

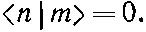(9.68)

Это выполнится автоматически, если все энергии различны. Кроме того, можно умножить все а i ( n) на подходящие множители, чтобы все состояния были отнормированы: чтобы для всех n было

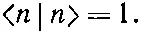(9.69)

Когда оказывается, что (9.63) случайно имеет два (или больше) одинаковых корня с одной и той же энергией, то появляются небольшие усложнения. По-прежнему имеются две различные совокупности а i , отвечающие двум одинаковым энергиям, но состояния, которые они дают, не обязательно ортогональны. Пусть вы проделали нормальную процедуру и нашли два стационарных состояния с равными энергиями. Обозначим их |μ> и |v>. Тогда они не обязательно окажутся ортогональными: если вам не повезло, то обнаружите, что

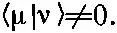
Но зато всегда верно, что можно изготовить два новых состояния (обозначим их |μ'> и |v'>) с теми же энергиями, но ортогональных друг другу:

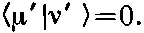(9.70)

Этого можно добиться, составив |μ'> и |v'> из подходящих линейных комбинаций |μ> и |v> с так подобранными коэффициентами, что (9.70) будет выполнено. Это всегда полезно делать, и мы будем вообще предполагать, что это уже проделано, так что можно будет считать наши собственноэнергетические состояния | n> все ортогональными.

Для интереса докажем, что когда два стационарных состояния обладают разными энергиями, то они действительно ортогональны. Для состояния | n> с энергией Е n

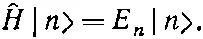(9.71)

Это операторное уравнение на самом деле означает, что имеется соотношение между числами. Если заполнить недостающие части, то оно означает то же самое, что и

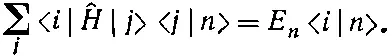(9.72)

Проделав здесь комплексное сопряжение, получим

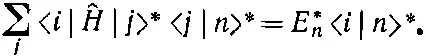(9.73)

Теперь вспомним, что комплексно сопряженная амплитуда — это амплитуда обратного процесса, так что (9.73) можно переписать в виде

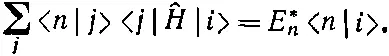(9.74)

Поскольку это уравнение справедливо для всякого i , то его можно «сократить» до

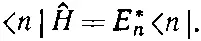(9.75)

Это уравнение называется сопряженным с (9.71).

Теперь легко доказать, что Е n — число вещественное. Умножим (9.71) на < n |. Получится

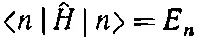(9.76)

(с учетом, что =1). Умножим теперь (9.75) справа на | n >:

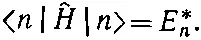(9.77)

Сравнивая (9.76) с (9.77), видим, что

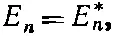(9.78)

а это означает, что E nвещественно. Звездочку при Е n в (9.75) можно убрать.

Теперь наконец-то мы в силах доказать, что состояния с различными энергиями ортогональны. Пусть | n > и | m > — пара базисных состояний с определенными энергиями. Написав (9.75) для состояния | m > и умножив его на | n >, получим

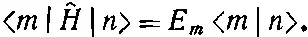
Но если (9.71) умножить на

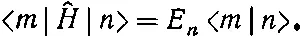
Раз левые части этих уравнений равны, то равны и правые:

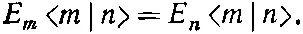(9.79)

Если Е m = Е n , то это равенство ни о чем не говорит. Но если энергии двух состояний | m > и | n > различны ( Е m ≠ Е n ), то уравнение (9.79) говорит, что < m | n > должно быть нулем, что мы и хотели доказать. Два состояния обязательно ортогональны, если только Е n и Е m отличаются друг от друга.

В этой главе мы займемся «сверхтонким расщеплением» водорода — интересным примером того, что мы уже в состоянии делать с помощью квантовой механики. Здесь у нас уже будут не два состояния, а больше. Поучительность этого примера в том, что он познакомит нас с методами квантовой механики, применяемыми в более сложных задачах. Сам по себе этот пример достаточно сложен, и как только вы поймете, как с ним справляться, вам сразу же станет ясно, как обобщить его на другие возможные задачи.

Как известно, атом водорода состоит из электрона и протона; электрон сидит неподалеку от протона и может существовать в одном из многих дискретных энергетических состояний, в каждом из которых его картина движения другая. Так, первое возбужденное состояние лежит на 3/ 4ридберга, или на 10 эв , выше основного состояния. Но даже так называемое основное состояние водорода на самом деле не является отдельным состоянием с определенной энергией, ибо у электрона и у протона есть спины. Эти спины и ответственны за «сверхтонкую структуру» в уровнях энергии, которая расщепляет все уровни энергии на несколько почти одинаковых уровней.

Спин электрона может быть направлен либо вверх, либо вниз; у протона тоже его собственный спин может смотреть вверх или вниз. Поэтому на всякое динамическое состояние атома приходятся четыре возможных спиновых состояния. Иначе говоря, когда физик говорит об «основном состоянии» водорода, он на самом деле имеет в виду «четыре основных состояния», а не просто самое низкое из них. У четырех спиновых состояний энергия не совсем одинакова; имеются небольшие сдвиги по отношению к тому, что наблюдалось бы в отсутствие спинов. Эти сдвиги, однако, во много-много раз меньше, чем те 10 эв , которые лежат между основным состоянием и следующим более высоким состоянием.