Ричард Фейнман - Том 3. Квантовая механика

Попробуйте (просто для упражнения) обратить наши формулы. Можно ли представить состояние |х> в виде линейной комбинации правого и левого? Да, вот ответ:

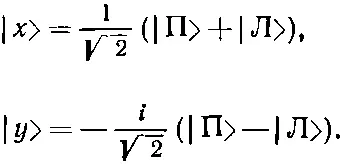(9.35)

Доказательство : сложите и вычтите два уравнения в (9.34). От одного базиса к другому очень легко переходить.

Впрочем, одно замечание надо бы сделать. Если фотон поляризован по правому кругу, он не имеет никакого касательства к осям х и у . Если бы мы взглянули на него из системы координат, повернутой вокруг направления полета на какой-то угол, то свет по-прежнему был бы поляризован по кругу; то же с левой поляризацией. Право- и левополяризованный по кругу свет при любом таком повороте одинаков; определение не зависит от выбора направления х (если не считать того, что направление фотона задано). Великолепно, не так ли? Для определения не нужны никакие оси. Куда лучше, чем х и у ! Но, с другой стороны, не чудо ли, что, складывая левое и правое, вы в состоянии узнать, где было направление x ? Если «правое» и «левое» никак не зависят от х , как же получается, что мы можем сложить их и вновь получить x ? На этот вопрос можно частью ответить, расписав состояние |П'>, представляющее фотон, правополяризованный в системе координат х ', у '. В этой системе мы бы написали

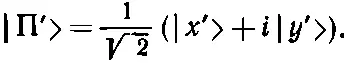
Как же будет выглядеть такое состояние в системе х, у ? Подставим | х '> из (9.33) и соответствующее | у '>; мы его не выписывали, но оно равно (-sinθ)| x >+(cosθ)| y >. Тогда

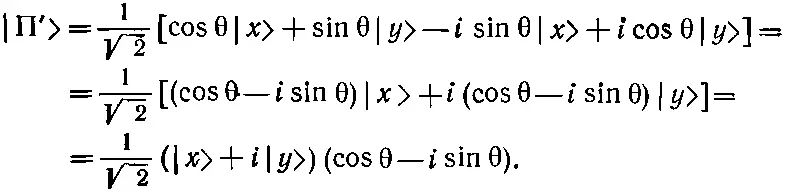
Первый множитель — это просто |П>, а второй е - i θ; итог таков:

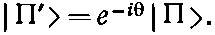(9.36)

Состояния |П'> и |П> отличаются только фазовым множителем е - i θ. Если подсчитать такую же вещь для |Л'>, мы получим [30] Это похоже на то, что мы обнаружили (в гл. 4) для частиц со спином 1 / 2 , когда поворачивали систему координат вокруг оси z; тогда мы получили фазовые множители exp (±iφ/2). В действительности это в точности то же самое, что мы писали в гл. 3, § 7, для состояний |+> и |-> частицы со спином 1, и это не случайно. Фотон— это частица со спином 1, у которой, однако, нет «нуль»-состояния.

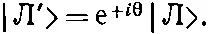(9.37)

Теперь мы видим, что происходит. Сложив |П> и |Л>, мы получаем нечто отличное от того, что получилось бы при сложении |П'> и |Л'>. Скажем, x -поляризованный фотон есть [см. (9.35)] сумма |П> и |Л>, но y -поляризованный фотон — это сумма со сдвигом фазы первого на 90° назад, а второго — на 90° вперед. Это просто то же самое, что получилось бы из суммы |П> и |Л'> при определенном выборе угла θ=90°, и это правильно. В штрихованной системе x -поляризация — это то же самое, что y -поляризация в первоначальной системе. Значит, не совсем верно, что поляризованный по кругу фотон выглядит в любой системе осей одинаково. Его фаза (фазовое соотношение между право- и левополяризованными по кругу состояниями) запоминает направление х .

Теперь мы расскажем о двухуровневой системе из мира странных частиц — о системе, для которой квантовая механика приводит к поразительнейшим предсказаниям. Полное описание этой системы потребовало бы от нас таких знаний о странных частицах, каких у нас пока нет, поэтому, к сожалению, кое-какие углы нам придется срезать. Мы лишь вкратце успеем изложить историю того, как было сделано одно открытие, чтобы показать вам, какого типа рассуждения для этого потребовались. Началось это с открытия Гелл-Манном и Нишиджимой понятия странности и нового закона сохранения странности . И вот когда Гелл-Манн и Пайс проанализировали следствия из этих новых представлений, то они пришли к предсказанию замечательнейшего явления, о котором мы и хотим повести речь. Сперва, однако, нужно немного рассказать о «странности».

Начать нужно с того, что называется сильными взаимодействиями ядерных частиц. Существуют взаимодействия, которые ответственны за мощные ядерные силы, в отличие, например, от относительно более слабых электромагнитных взаимодействий. Взаимодействия «сильны» в том смысле, что если две частицы сойдутся так близко, чтобы быть способными взаимодействовать, то взаимодействуют они очень мощно и создают другие частицы очень легко. Ядерные частицы обладают еще так называемым «слабым взаимодействием», в результате которого происходят такие вещи, как бета-распад; но они всегда происходят очень медленно (по ядерным масштабам времени): слабые взаимодействия на много-много порядков величины слабее, чем сильные, и даже слабее, чем электромагнитные.

Когда при помощи больших ускорителей начали изучать сильные взаимодействия, все были поражены, увидев, что некоторые вещи, которые «должны были» произойти (ожидалось, что они произойдут), на самом деле не возникали. К примеру, в некоторых взаимодействиях не появлялась частица определенного сорта, хотя ожидалось, что она появится. Гелл-Манн и Нишиджима заметили, что многие из этих странных случаев можно было объяснить одним махом, изобретя новый закон сохранения: сохранение странности . Они предположили, что существует свойство нового типа, связываемое с каждой частицей, — число, названное ими «странностью», — и что во всяком сильном взаимодействии «количество странности» сохраняется.

Предположим, например, что отрицательный K -мезон высокой энергии, скажем с энергией во много Гэв , сталкивается с протоном. Из их взаимодействия могут произойти много других частиц: π-мезонов, K -мезонов, Λ-частиц, Σ-частиц, — любые из мезонов или барионов, перечисленных в табл. 2.2 (вып. 1). Оказалось, однако, что возникали только определенные комбинации , а другие — никогда.